I would like to present something I have been working on a little while. Like I mentioned in the other thread (TSR vs glide ratio - #4 by tallakt) I believe maybe HAWT having a TSR of around 9 could be matched by a AWE rig where the overall glide ratio (tether and kite) is above 6. To have a competitive advantage, perhaps aiming for 8:1 overall is a good start, maybe increasing to 10:1 or better later if that was achieved first.
Edit: After @dougselsam 's comment I realized that TSR and glide number should match 1:1.
Note I’m thinking about any AWE rig having single kites flying on single tethers here (eg Kitemill or Ampyx), not other kids of rigs.
So I start with just a tether of diameter 3 mm, then assume it has a zero drag kite attached to it, pulling the ultimate strength of the tether divided by a safety factor 4 at a certain windspeed. Then I assume the kite will fly at a speed being the product of overall glide ratio, wind speed and an elevation angle of 25 degrees.
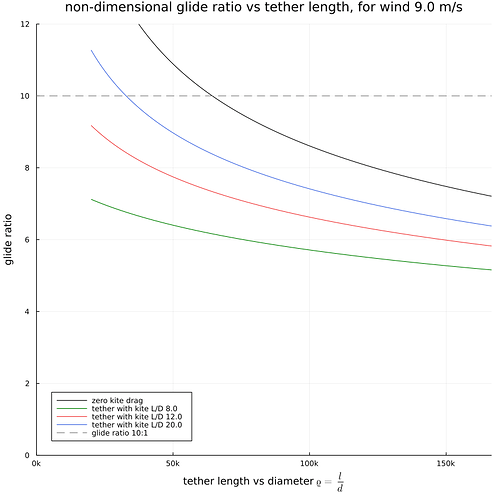
By using almost no information about the kite, we can see a ceiling glide number achieveable using only tether and a super efficient kite. In short, this ceiling depends on the tensile yield modulus of UHMWPE rope and tether drag coefficient (I use 1.1 here)
I also extend this for kites with a certain L/D ratio.
Anyways; please ask for more questions in the thread if you want. I will attach the source code to produce the plot for any super curious people out there. The result is that you can see from the plot that if you want a certain overall glide ratio, there is a certain maximum possible tether length that could be used, unless you can reduce tether drag somehow. And if the overall glide ratio is high, the tether length is not terribly long.
As I made the plot dimensionless, we see eg. for a kite with glide number 20:1 [blue curve] and a goal overall glide ratio of 10:1 [gray dashed line], the value of \varrho should be 35k. To calculate the actual tether length, if the tether diameter is 3 mm, the length is
l = 0.003 \cdot 35.000 = 105 \,\mathrm{m}
If we settle for a glide ratio of 8:1, the tether length of that rig would be \varrho = 75k or 225 m. This would match a kite like Ampyx AP2 with a wingspan of 5-6 m.
Finally, I will again state my feeling that a higher efficiency (overall glide ratio) vs a HAWT TSR is one of the most interesting ways in which an AWE rig can outperform for lower cost.
glide_ratio_ceiling.jl (3.0 KB)
Edit: I updated the plot and numbers as I had by mistake used a drag coefficient too small, not 1.1 for the tether