Cubic scaling of tether mass as a critical limit to scaling

Engineering Math & Physics
1

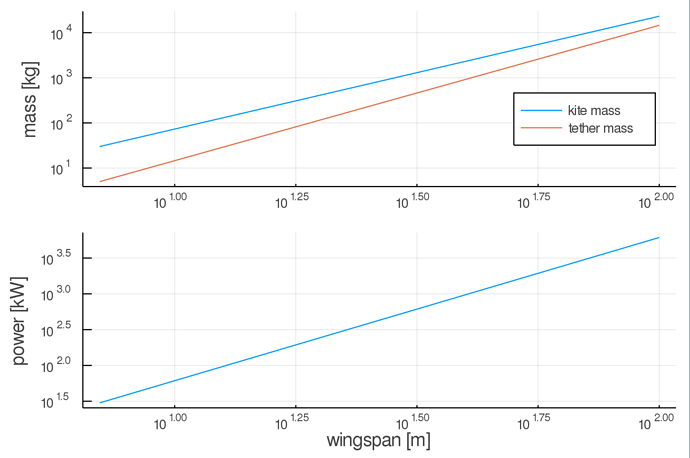
Edit: started out with the wrong mass per meter. Adjusted from 18 kg to 5 kg. Updated plots

I’d like to discuss this. For a wingspan b we may scale out AWE rig into a bigger one with wingspan x b. By doing so, power scales by x^2 as lift depends on wing area. Tether diameter must scale by x to acomodate the increased pull force of the kite. The kite mass will scale somewhere in the range x^2 \lt x^y \lt x^3, I’ll assume y \approx 2.5.

These things should be fairly well known for AWE.

Furthermore, I state that tether length should scale by x. This ensures that the flight characteristics are preserved and also preserves the geometry of flight. I will not show why I believe so here, just state it as an assumption.

The mass of the tether must be lifted by the kite. A tether of 400 meter 4 mm weighs approx 5 kg. This would be suitable for a 30 kW rigid kite (I think rigid vs soft does not matter in this case, but feel free to comment on this).

We stated that y is 2.5 rather than pure cubic scaling because in designing a structure, some things could be easier with larger scale (eg, the distance between the top and bottom of an I-beam increases, as seen on https://www.amesweb.info/SectionalPropertiesTabs/SectionalPropertiesIbeam.aspx). Scaling of a kite must scale both beam structures and skin structures, and finding a simple equation for this is not easy.

The mass of the tether though is quite straightforward to calculate, and it scales cubic by x^3. There is really no way to get around this. Hence I am thinking that the weight of the tether could be the ultimate scaling limit for AWE.

I have added a simple plot for reference. It is just meant as an illustration, not based on an accurate calculation.

image
image1798×1194 144 KB

The conclusion to this would be that if you want to go bigger than current HAWT (in power output), you may have to focus on designs with relatively shorter tethers.

Another conclusion would be that conductive tethers and flygen are at a big disadvantage.

A third conclusion would be that TRPT is looking better than ever :wink:

1 Like
2

You mean the longer the wingspan the longer the tether? So if original tether length is l, you get x l after you change wingspan to xb?

With proof and explanation given, I could probably see how that could work in current yoyo systems. I don’t see how that would work for some other systems. How about for spidermills? I would think for those you could choose altitude based on windspeeds, except if you have a very thick tether you maybe would need a very large drum if you want to go high.

3

Exactly.

I think for any design the fundamentals are the same. But each design must be proven separately… after revisiting my initial tether mass estimate that was wrong, the scale for Yoyo now works fine until approx 10-100 MW output. This is big enough for most people to not care I think.

The principle though remains true… Eg: If someone should say 1 GW, this should be taken into account.

4

A practical scaling limitation on tether diameter is surface damage by its own mass. Surface abrasion resistance remains constant as tether mass is increased. A too-thick working tether therefore faces excess abrasion forces from simple handling events. Anti-UV/abrasion sheathing is a possible help.

~5cm diameter is a conservative bet for a scalable-by-number tether diameter that is large enough for serious unit-rating, without over-scaling to excess surface-abrasion.

5

That (5 cm tether) coincides pretty well with where a tether will out-mass a rigid kite.

I would think for a soft kite, the tether is relatively much heavier. Lightweight, slow moving kite, with relatively large pull… Perhaps for soft kites, tether mass would be a big issue even before 1 MW scale… Would be an interesting analysis to perform… (edit: Im not thinking clearly here - soft kites are probably also cubic scaling in mass. The kite weight will escalate in mass the same speed as the tether)

1 Like
6

On the other hand, high-mass high-velocity single-line kiteplanes are inherently more dangerous (under aviation mass-velocity categories), requiring a greater tether safety-factor, compared to multi-line power kites. Kiteplane designers tend to skimp on tether safety-factor, to reduce exponential drag at high-velocity.

Also, a huge power kite kept under the same altitude limit (ie. ~600m) is proportionally “short-lined” (non-dimensional tether length) compared to a smaller kiteplane of equivalent mass.