Riffing off of Moritz’s AWEC2021-22 Presentation-
About Circular AWE Farms With High Surface Power Density (Moritz Diehl, Jakob Harzer, Jochem De Schutter), from the book of abstract AWEC2021, and also in the technical program:
http://resolver.tudelft.nl/uuid:8763994b-763a-4990-b666-ab75b99060c6
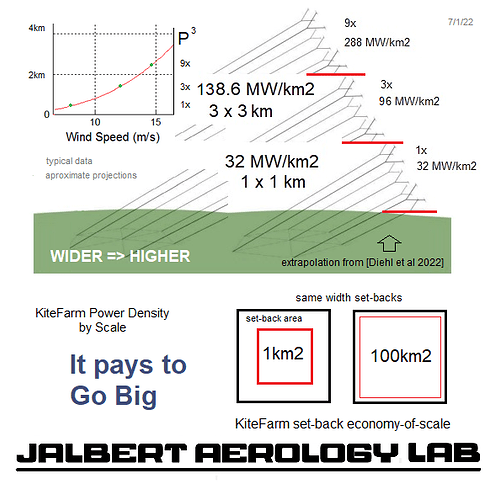
From the drawing it looks like the density is considered in regard to the ground hexagon with the seven unities. But if we consider the given elevation angle of 30 degrees, then the whole swept area (also about 1 km², so more than 1 km diameter) the length of the tethers of the upper devices could be more than 2 km, while the tethers of the lower devices are further away from the center. To be conservative that leads to a circle of at least 1.5 km radius, so a ground area of 7 km². If we take into account of the required safety zone in case of crash, say 20 km² for the whole, the density drops from 32 MW/km² to less than 2 MW/km² which is the existing wind power farm density, and this without allowing easy secondary use. Of course the reliability and the efficiency of all this stuff remains to prove: real average power, risks of collisions and crashes, wind irregularities within the farm that cannot always be controlled…
Now considering extrapolation, the higher the altitude, the stronger the winds, but also the heavier the AWES tethers and the more drag they generate.
All this literature on the immense possibilities of AWE reminds me of a fable by Jean de La Fontaine:
“La Laitière Et Le Pot Au Lait”
Perrette, on her head having a pot of milk
Well-placed on a little cushion,
Was intending to get without problem to the town.
Dressed lightly and short, she went with long strides,
Having put on that day, so she’d be more agile,
Simple garments and flat shoes.
Our milkmaid so attired
Counted already in her thought
The income from her milk; was using the money;
Bought a hundred eggs; had a triple brood of chickens.
Everything was going well thanks to her diligent care.
“It is, she said, easy for me
To raise chickens about my house.
The fox will be very skilful
If he doesn’t leave me enough to have a pig.
The porker to become fat won’t take much bran;
He was, when I got him, of reasonable weight:
I will have, when I sell him, fine and good money.
And who can stop me from putting in our stable,
Considering the money I will have, a cow and her calf,
Whom I will see leap about among the herd?
Perrette on this thoughts, leaps also, carried away:
The milk falls; goodbye calf, cow, pig, chickens.
The lady of all these goods, leaving with sorry eye
Her fortune hence spread out,
Goes to ask forgiveness to her husband,
With a good chance of getting slapped.
The story was made into a farce:
It was called the Pot of Milk.
Several factors combine to refute “pot of milk” emotional pessimism that Moritz’s principle starts marginal by line drag or mass and cannot be extended.
-
a single kite on a single line can carry up several kilometers of line, as proven for centuries.
-
a giant kite network can have short tether proportions.
-
a thicker tether’s strength to drag is better as cross-section increases roughly at the square of diameter and cube of surface area.
-
JAL proposes topologically-stabilized Kite Networks, without avionics mass-aloft, instead of the tricky-to-control “brush”-topology, with avionic mass-aloft dependence Moritz presumes. Less mass means more power from higher altitudes.
-
What a terrible nursery text to teach French children misogyny and justify male violence toward women. It’s not a sound AWE engineering-science analogy either.
This analysis is unrealistic because the crosswind velocity of each kite must be limited at higher wind velocities. Assume conservatively that the effective wind velocity is three times the actual wind velocity.
At a height of 0.7 Km, wind velocity = 5 m/sec, effective wind velocity = 15 m/sec.
At a height of 1.3 Km, wind velocity = 12 m/sec, effective wind velocity = 36 m/sec
At a height of 2.5 Km, wind velocity = 14 m/sec, effective wind velocity = 42 m/sec
The above are average wind velocities and so crosswind action must be curtailed for most of the time at the higher altitudes.
Crosswind velocity is always limited, no matter what wind velocity.
JAL analysis departs from Moritz’s local load motion (twin-kite) assumptions to include bulk motion of all units as a many-connected network.
As such a bulk network dances back and forth, the lower part does indeed “wag” more than the top, just as you suggest natural.
In Moritz’s special case of many twin-kites-on-single-tether, either higher flygen drag or higher AoA can extract the higher power at the top without violating a crosswind velocity limit.
The key “realistic” insight is that going somewhat higher over a wider footprint than Moritz defines promises to pay off in higher spatial density.
If you are proposing something different to Diehl et all
then there’s no need to extrapolate from their scheme,
Just propose the JAL scheme.
A few issues which Diehl et all considered in their scale…
There will be severe demands on handling the whole field anchoring of a scheme this size.
Every anchor changes length with wind direction to maintain the whole frontal meta kite shape.
A change of wind requires a lot of winching to kick in quickly if you want to avoid the short front long back configuration. (Then again, assuming good control can be developed a mass expansion pattern on realigning… might be fine)
The constant setback advantage you depicted seems very unlikely now that you have blades at higher altitudes, faster in stronger winds.
The depiction of a wind shear graph - way off - much steeper lines there - High altitude is not the attraction it once seemed to be in AWES.
It is proposed that Moritz’s idea applies to both his twin-kites example and many-connected kites. JAL favors a many-connected topology consistent with Moritz’s analysis, which was conservative with regard to max altitude.
Greater altitude is a specific AWE advantage over hardware bolted to a pole. Some AWES archetypes are indeed severely challenged to work higher than a tower, but not all. Kite Trains and layered Networks easily reach 3km; more or less the sweet spot Cristina identified.
The setback advantage to wider kitefarms is general. Greater width is presumed not to require a wider setback once altitude limits kick in.
Let others believe otherwise. Future developments will settle doubts.
It really would help to show your own image of What you mean here. How a many-connected scheme relates if it is not the same as the Diehl et al scheme
Setback for wider farms is general? What does that mean? There is no justification to say it can be proportionately less when you mention high altitude and then also … some altitude limit kicks in… OK then Where does this single layer wide field slope scheme get it’s height?
Is it sloped sides a flat level top and center area? State that please. Because that could limit setback, but not increase altitude.