Gravity and bellying of the tether

[tallakt]

Edit: replaced convex with concave
Edit: For bounding [yoyo] the tether drag of a straight tether is 1/4 of full tether drag

Hi. I think it’s fascinating that even after all these years there are still some new things to be said about AWE even using only the simplest analysis. Today I wanted to share something I have been working on related to tether drag.

So the starting point is a kite flying in a circular path. The tether may as a first approximation be regarded to be a straight cylindical body, and we can calculate the aerodynamic drag to be something like

D = \frac{1}{4} \frac{1}{2} \rho v_k^2 C_D l d

Where
\rho - density of air
v_k - forward speed of the kite
C_D - drag coefficient of the tether, usually close to 1.0
l - tether length
d - diameter of the tether

We see that the drag is a certain fraction of the drag of the tether as though all of it was travelling at the speed of the kite. We are disregarding wind here, because the kite speed v_k should ideally be higher than the wind, and the wind blowing a lot along the tether, so the drag effects caused by moving forward should dominate those caused by wind.

Also as a general thing to keep in mind - most of the drag is generated close to the kite, because drag is determined by airspeed squared. The tether is moving fast at the kite, and standing still at the ground.

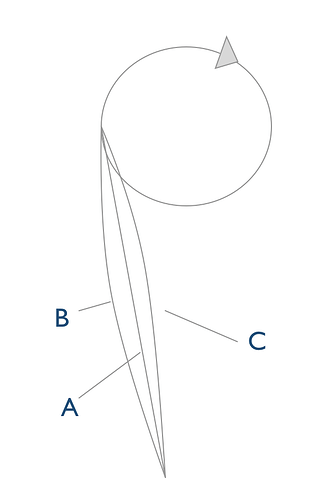
Now I will make things slighty more complicated; The tether is not really straight. I have drawn a sketch

Slice.pdf (7.5 KB)

The scenario we were talking about before is labeled “A”. But the tether is long and bends easily, so it may have a “belly” like “B” in the figure, or more of a concave shape like “C”. (in addition of course to an infinite amount of more complex shapes)

If the tether has a belly, the looping radius of the tether would be larger, and thus the airspeed at the tether will increase. If we combine this information with the previous assertion that most drag is generated close to the kite, we see that even a slight amount of “belly” can increase the tether drag observed by the kite significantly. (Thought experiment, the bellying shape can be approximated by a new straight tether being much longer and tangential at the kite to the real tether. The drag would be close to that of the long straight tether)

So I have had the “goto” thinking that the reason for a belly would be the centrifugal forces on the kite. So, smaller looping radiuses, less tension and heavier tether would be the main causes for getting a belly. Also, if you scale the tether naturally (b \propto l \propto d, with b being the kite wingspan), the tether will get relatively heavier with scale and the bellying effect get more and more pronounced.

I had a poster on this subject at AWEC 2019 https://www.researchgate.net/profile/Espen-Oland/publication/336617086_THE_SECOND_MOST_IMPORTANT_LAW_OF_TETHER_SCALING/links/5da8bc5a92851c577eb7fb9f/THE-SECOND-MOST-IMPORTANT-LAW-OF-TETHER-SCALING.pdf?origin=publication_detail

My conclusion at that point was that hovering systems with conductive tether like Makani were pursuing back then was going to have tangible scaling issues because their tether mass and bellying already was an issue at the current scale.

–

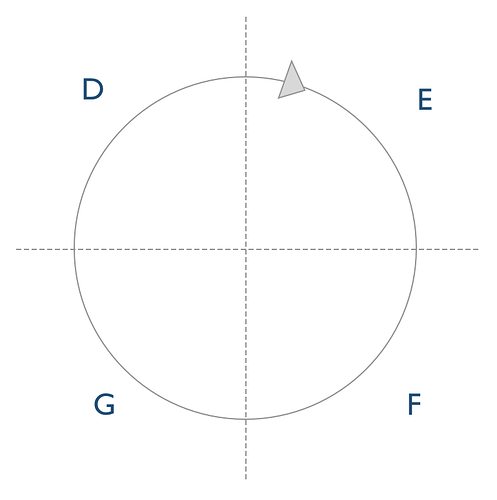
Ok, that was more of a background story. The new thing is that “doh”, gravity also has a huge impact on bellying and concavity of the tether. In fact, I would like to divide the loop into four quadrants to identify the impact of tether drag and gravity, being two very important influenced on flying speed of the kite.

To go through each quadrant, with all effects being due to gravity:

D - Concave tether, kite slowdown
E - Concave tether, kite speedup
F - Bellying tether, kite speedup
G - Bellying tether, kite slowdown

The effect on tether bellying is variable based on tether length, mass, scale, tension etc. But I do believe the tether drag could vary to a near zero of the “straight” tether drag somewhere in quadrant D and E, and somewhere near double in the quadrants F and G.

What are the consequences? I think overall good, because you get more help in the difficult D quadrant, where gravity is slowing down the kite, but the reduction in tether drag will compensate somewhat.

Also, but to a lesser extent, the effect is helping in quadrant F and G where you may get overspeeding issues in higher winds. The tether drag will increase. Though it is never a good thing, but it is the best place it could happen.

[Windy_Skies]

If the cross-section of the path of the kite is a circle, the cross-sections of the idealized path of the tether from kite to ground are smaller and smaller circles. With equal speed of the kite and tension on the tether but now with the effect of gravity, the cone would now sag down a little, but the shape of the individual cross-sections would stay the same, I think.

With now here a lower kite speed and lower tension at the top of the circle for the kite, now the cross-section of the tether path changes, it becomes flatter at the top of the circle, so there the tether is moving relatively slower than the kite. At the points along the circle where the kite speed is highest and tension is highest, tether sag due to gravity should be lowest and the path of the tether should match that of the kite relatively closely. I don’t see where the path of the tether becomes relatively longer than that of the kite, so I don’t see where the tether is moving relatively faster than the kite.

[tallakt]

I will be simulating this over the next few weeks… curious to see what comes out. The fact that the tether has a 3D shape somewhat lagging the kite coordinate complicates things a little.

But your arguments are good and you may well be more right than me

[tallakt]

The plot fives an indication of how the drag force can vary. I didn’t “anonymize” the plot, just to sloppy to add proper time scale and such. Anyways the plot is a simulation of a tether 3 mm diameter, 500 m long, flying at elevation 30 degrees, 40 m/s in a circular loop on constant tether length, wind 12 m/s from north. Looping in direction south.

The simulation is unverified.

But if we assume the plot is accurate, we do see the drag varies quite a bit for a kite flying at constant speed (the kite itself is not simulated, rather the kite path is preprogrammed).

Anyways, the blue plot is without gravity, the red one is with gravity. So the effect of gravity on drag in this plot is pretty minor, and also it counterintuitively (for me) has an effect to decrease the variation in drag.

I would expect this is related to the tension not being constant though.

The reason for drag variation would be probably the wind…

[Windy_Skies]

@tallakt

The reason for drag variation would be probably the wind…

This seems like such a basic question. Hasn’t this been researched already?

I think it’s difficult to say anything about the graph without knowing say what points in the kite trajectory line up with which points in the graph, what equations/model were used to generate it, and the scale compared to the aerodynamic drag.

If we assume the graph is somewhat correct and the wave is due to the wind, then one guess could be that the tops, where drag is lowest(?), correspond to those points where the wind is helping… But if you look at it like a unit circle with the kite turning counterclockwise, disregarding elevation angle, that should happen, at least, 4 times per rotation? At 90 degrees sin(y) doesn’t change much and cos(x) rapidly goes to 0, at 180 degrees sin(x) doesn’t change much and sin(y) rapidly goes to 0… But you didn’t disregard elevation angle and still got what looks like an unvarying wave. But a circle has rotational symmetry, so this guess shouldn’t be right anyway.

At the bottom of the loop, now not disregarding elevation angle, the surface area of the tether exposed to the wind is lower than at the top, and elsewhere, so you’d perhaps expect the amplitude of the wave to be lower there. Or perhaps correspond to those places where drag due to wind is lowest.

Please correct me in the likely case I am wrong about all of this.