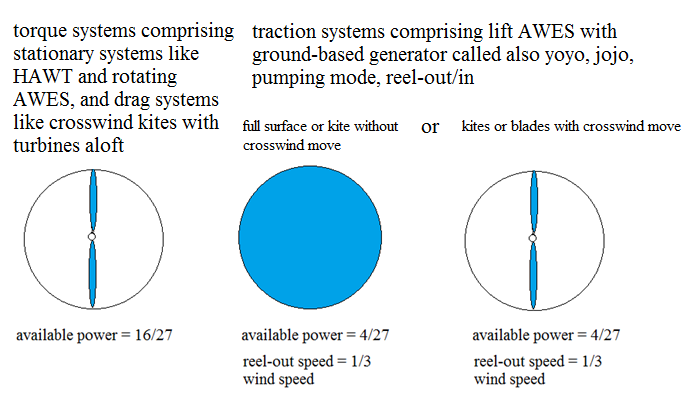
“AWE drag power systems can harvest up to 16/27 of the power available in the wind.
AWE lift power systems can harvest up to 4/27 of the power available in the wind.”
A drag power system has the turbines aloft like a Makani’s wing.
A lift power system has a ground-based generator and is a pumping kite system (yo-yo, jojo, reel-out/in…).
My first comment: practically this large difference is not so significant because the area swept by both (for example Makani and Ampyx) exceeds several times the useful swept area. But it can be different if the swept area is maximized with several wings like “dancing kites”.
The result as 16/27 can favor drag power systems (Makani, FlygenKite…), horizontal-axis turbines (HAWT), and generally rotating devices like Rod’s Daisy or Rotating Reel or autogyro-like (https://www.youtube.com/watch?v=gExAQq2VzgQ). All these devices have a stationary rotor and convert wind power by using torque, while lift power devices (yoyo) use traction.
Let us try to check this with an example, wind speed = 10 m/s, air density = 1.2.
The power of a HAWT is determined by the disk swept by the rotor. Supposing the disk area is 100 m².
Power at Betz limit: 1/2 x 100 x 1.2 x 1000 x 16/27 = 35555 W.
Now let us take a surface of 100 m². Traction (force): 1/2 x 100 x 1.2 x 100 = 6000 N. Let us reel-out this surface in the optimal speed of 1/3 wind speed, considering the wind speed on the surface is now only 2/3 wind speed, leading to the result: 20000 x 4/9 = 8888 W, so exactly 1/4 of 35555 W.
Checked!
Isn’t that wrong, considering that the speed of the kite is not 10 m/s, nor is the area of the kite 100 m^2. Would you mind elaborating how you got the numbers?
Assuming both 100 m² surface (kite-like with only drag) and disk area (horizontal-axis turbine (HAWT)) are perpendicular to the wind direction.
The surface goes downwind during reel-out phase (jojo = lift mode here) without flying, with only a horizontal translation. The surface and its tether reeling speed is 1/3 wind speed. 1/3 wind speed is the generally seen as the optimal tether speed in order to maximize the wind power for yoyo mode.
Now considering the surface is smaller, its area being something like 10 m². If its zeta factor is high enough (10 if I am not wrong), it will sweep the100 m² in crosswind mode (its speed being several times the wind speed), producing 8888 W as previously while the tether reeling speed will be 1/3 wind speed as previously.
For this comparison 100 m² is also a wind area. In drag mode (HAWT) “Betz limit” is a correct expression as the 100 m² (more in a real world) wind area crosses the 100 m² disk area. In lift mode, a 100 m² wind area cannot cross the 100 m² surface taken alone, but a larger wind area can… Perhaps the author uses the expression “power available in the wind” as an alternative to “Betz limit”.
I don’t think my demo is scientifically correct contrary to the paper, but is a simple mean to check it.
1/3 wind speed downwind leads to (1/3)², so 4/9 available power. It is due to the lower apparent wind speed², 10² becoming ((2/3)10)².
I am thinking about this and I’m not sure if you can just multiply Betz’ limit with reel out speed like this, because the starting point for making Betz’ law are no longer the same with a JoJo AWE rig.
Why? because we are reeling out, the air escaping the windmill will at minimum have the speed equal to reeling out speed. Thus if you look at it from this point of view, the wind escaping this AWE rig will have exactly the same speed as the air escaping the ideal windmill from the derivation of Betz’ limit.
If I am right here, the Betz’ limit probably applies 1:1 to both Jojo and drag based AWE.
BTW: No, I didnt read the paper behind the paywall.
https://www.researchgate.net/publication/324448503_The_Betz_limit_applied_to_Airborne_Wind_Energy then click on request full-text.
Betz’ law is difficult to apply for pumping mode as the swept area moves with the tether going downwind.
But the examples I provide sound correct in some way and can be verified by experimentation: using a static kite of for example 1 m², that with a given wind speed, elevation angle close to 0°, then measuring tension (force) in static position, then the resulting tension by reeling-out by 1/3 wind speed, becoming 4/9 the initial tension, then the power by multiplying the resulting tension by reel-out speed (1/3 wind speed). Both paper and my calculations (I use power = force in static x 4/9 x 1/3 wind speed) give 4/27 as limit. Now measuring the power of a 1 m² wind turbine: the limit is 16/27, the well-known Betz limit.
In the real world the area swept by the kite is far higher as the useful swept area. So if Kitemill’s wing becomes a drag kite (like Makani’) it will not be necessarily more efficient. But the wind area that is harnessed could be smaller.
“Abstract
In this paper we revisit the modeling framework used to derive the Betz limit of power extraction from the wind based on linear momentum theory. One of our contributions is to suggest that the Betz limit of 16/27≈59% should in fact hold true for any device that harvests power through drag or torque in a horizontal-axis rotational motion perpendicular to the wind field, which is not only the case of conventional wind turbines but also of Loyd’s drag power Airborne Wind Energy (AWE) systems. Another contribution is to show that Loyd’s lift power AWE devices during the reel-out phase can harvest up to 4/27≈15% of usable power available in the wind, i.e. exactly 1/4 of the theoretical limit of the horizontal-axis turbines and AWE drag power systems with ideal airfoils. Moreover, in order to operate at such limit, AWE lift power systems must also extract from the wind an amount of drag power that is equal to the reel-out power. These claims are supported by physical principles and mathematical formulations.”
HAWT, rotating AWES, AWE drag power systems (Makani-like): all use torque (even Makani of which turbines onboard are secondary turbines) and are stationary systems as their respective swept area is stationary.
Lift power systems are tension (or force or traction) systems: they use tension (or force or traction) and are unstationary.
I think I probably agree with the conclusion. Betz’ limit is an upper bound to generated power. It would be interesting to know how soon the efficiency difference between lift and drag based AWE will manifest itself, if all other conditions are equal (ie same wing, same radius, working at optimal speed and reel-out)
There is no reel-out phase for drag based AWE as their swept area is stationary.
IMHO in a first approximation the efficiency of lift and drag power systems could be similar with a same wing, but lift power systems should use 4 times the swept area used by drag systems achieving Betz limit, that without taking account of the reel-in phase (energy and time expenses).
I disagree that there is substancial difference between lift and drag force AWE. I agree that the Betz limit is different for the two though. The Betz limit may also be thought of at something happening when you have kites covering the entire swept area, and each kite is more or less flying in the wake of the kite in front. This is probably far from the operational parameters of most AWE for some time yet.
My point is, the Betz limit happens at some point, and much earlier for lift force AWE, but until the limit is met, the two kinds og AWE have essentially equal utilization of wing area, producing almost exactly the same power for comparable units.
Drag mode adds a breaking force to the wing. The optimum value of this force makes the wing fly at approx 2/3 of maximum speed.
Lift mode, due to reeling out with optimum reeling out speed 1/3 of wind speed, reduces the wind speed to 2/3 og actual wind. The wing will fly as fast as possible in reduced wind.
The maximum speed of a wing is approximately given by v = G w. (G being glide number, w wind speed and v speed of wing relative to ground). We can assume that the power output is mostly dependent on how fast the wing is flying.
The drag mode AWE flying at v = 2/3 v_max = 2/3 G w
The lift mode flying at v = (2/3 w) G
They are the same…
All formula indicate a similar efficiency for both drag and lift (during reel-out phase) power AWES, but without mentioning the swept area.
One can roughly deduce the swept area of Makani M600 from the circling radius (135 m) that is given on some documents like http://www.energykitesystems.net/FAA/FAAfromMakani.pdf.
So the swept area could be something like 13000 m², so far more than 4 times the usual swept area for a 600 kW ground-based wind turbine. Perhaps such a circling radius (leading to the high swept area) is due to flight requirements (?). In these conditions the swept area would be about the same for both drag and lift power systems.
But if several M600 wings are arranged in the same swept area (13000 m²), things can be different as the Betz limit could be more approached, leading to a lesser space/land use.
From the paper, page 39: “…we proposed a generalization of the Betz theory by including a share of
power due to the downwind translation of the actuator disc, which can be seen as the tether reel-out speed".
Some experiment of a rotating kite on https://www.youtube.com/watch?v=0GflQyDDQec.
-
Wing area: 0.7 m²
-
Swept area: about 5 to 10 m², assuming 7.5 m²
-
Wind speed: 4 m/s
-
Measured tension: 40 N (becoming 60 N for large crosswind figures, far above the mentioned swept area), assuming wind speed ² = 16.
Now let us reel out with an optimal speed of 1.33 m/s. The apparent wind speed becomes 2/3 x 4 = 2.66 m/s; the wind speed² is multiplied by 4/9 = 7.11. So the tension is also multiplied by 4/9 and becomes 17.77 N.
The power is 17.77 x 1.33 = 23.63 W. Assuming the swept area is 7.5 m², the efficiency is (with air density = 1.2 kg) 8.2 % of the global wind power, and 13.9 % of Betz limit, close to the limit (15 %) of the available wind power according to the paper since a lift power system would be used.
So If I put a second same wing in the same swept area (7.5 m²) the power would not be higher. But these numbers (swept area above all) are very rough…
Its true. But I would be quite vary to put too much into these numbers because of
- very low wind speed, mass of kite is important
- serious deformation of the kite
- low quality measurement
Another wrong or right concern: for yoyo systems the swept area is partially renewed thanks to the vertical velocity.
An example: wind speed = 10 m/s; wing speed = 30 m/s; elevation angle = 30°; reel-out speed = 3.33 m/s; vertical velocity = 1.66 m/s; wing span = 10 m.
Assuming the path is a loop of which the circling radius is ten times (so 100 m) the wing span (as for Makani’s drag system), the time of a revolution is 10.46 m/s. During this time 17.37 m vertical distance travelled, involving in a correspondent part of “fresh air” for the next swept area. In some way one could estimate this increases a bit the initial swept area.
Of course this fast calculation is very rough (for example the cosine of the swept area is not yet taken into account).
To resume one rightly or wrongly could add that the vertical translation of the actuator disc leads to a bit larger swept area.