Betz limit and power available in the wind

Engineering Math & Physics
21

I agree, though the effect is probably marginal.

Also reel-out speed in the paper states reel-out in the direction of the wind. This is not a realistic scenario as elevation angle should be at least in the range of 20-30 degrees. The harvested power is made by multiplying the reel out speed and the tension of the tether, in the direction of the tether. I think this means that in theory you could produce a bit more than the lift mode Betz limit

I am not sure if these two statements both represent the same effect.

Im not sure if the effect is entirely positive though. We are saying that one wingtip will have fresh wind at the top of the spiral/fig8 while otherwise in the wake of previous wing. This will create additional stress on the wing.

BTW: I received the paper for free and it was a good read.

22

Recall: traction 6000 N X 1/3 wind speed = 20000.
Now assuming the elevation angle is 30°, leading to a cosine of 0.8660.
The reel-out speed in the horizontal becomes 2.955 m/s.
And the apparent wind speed becomes 10 - 2.955 = 7.045 m/s instead of 6.66 m/s.
7.045² = 49.63. Then 49.63/100 = 0.4963 instead of 4/9, so a bit more (10%).

23

IMHO the 4/27 of a flat plane is also the 4/27 of a same area swept by a lift (yoyo) crosswind kite as both go downwind.
Indeed an interesting Dave Lang’s message on https://groups.yahoo.com/neo/groups/AirborneWindEnergy/conversations/messages/6790 mentions:

So (at least by my derivation) for a device like a “parachute” or a “Ship on a down-wind run under sail”,

1. The Max power extraction fraction = “(4/27)* Cd”

2. Peak power extraction occurs at a “downwind device speed” of “(1/3) Vwind”.

OF course the devil is in the details concerning the value of Cd, since it is itself a quantified measurement of a device’s propensity to catch air. For instance, a flat plate has a Cd frequently quoted as about 1.1, Thus, a flat plate operating as a drag device to capture wind power, will exhibit the ability to extract only about 15% of the incident power (compared to the classical turbine limit of 59%).

24

Thanks for posting this talk in the Yahoo group @PierreB.

Moritz Diehl at AWEC 2015: Multiple Wing Systems - an Alternative to upscaling?

All of the talks from the conference are here:

http://www.awec2015.com/presentations.html

And AWEC 2017: http://awec2017.com/presentations-main.html

25

Hi would like to add a possibly new observation, that maybe should lead to a reevaluation of the 16/27 limit for hovering [drag] mode designs.

Because an AWE plant in general (especially if self-erect) will be rotating with the blades in a plane that is rotated according to the plant elevation angle, presumably in the range 20 - 40 degrees.

This means blades will be travelling slightly downwind sometimes and upwind sometimes. Slightly is maybe an understatement, as the speed may be to the order of 13% of blade ground speed. Though the effect is not linearly symmetric. For instance, blades travelling upwind will have wakes with larger spacing than those travelling downwind.

In short the actuator disc is not uniformly loaded at all. I believe this would lead to a further reduction of the Betz limit after 16/27, if one did thorough calculations

This affects bounding [lift] mode plants less, because these will presumably have active winch speed control to compensate for elevation angle. Still, the end result would be quite difficult to analyze, and probably no better than the 4/27 Betz limit already stated

1 Like
26

Isn’t it the cosine loss that we already know?

27

No. The cosine loss only deals with the geometric alignment of the kite vs power generation. This latest post regarded what happens when you approach the Betz limit. This would be a very interesting analysis to be done…

28

Also interesting question is whether cosine loss affects the Betz limit. I dont think it does, in general.

What I am talking about is uneven distribution of power over the actuator disk, and that some of the disk is moving upwind or downwind.

29

To see someone way ahead of me in terms of forward thinking about Betz limit in awe look to

An engineering model for the induction of crosswind kite power systems by Gaunaa et al

Abstract. The present paper introduces a new, physically consistent definition of effective induction that should be used in engineering models for power kite performance that use aerodynamic coefficients for the wing. It is argued that in such cases it is physically inconsistent to use disc-based induction models – like momentum models – and thus a new, physically consistent induction model using vortex theory methodology is derived. Simulation results using the new induction model are compared to the previously often used momentum method and Actuator Line (AL) CFD simulations. The comparison shows that the new vortex based model is in much better agreement with the AL results than the momentum method. The new model is as computationally light as the momentum induction method.

And

… , where the tip speed ratios are not too low (usually TSR>6) and where the aerodynamically effective part of the blades extend almost to the rotation axis. For the kite case, there is (usually) only one “blade” circling in the “rotor-plane”, and the effective “root” (inner kite tip) of the blade is often at 80%-90% of the radius of the “tip” (outer kite tip). In this case the Goldstein function would be immensely different from Prandtl’s tip correction, and it would be an extremely large correction to the raw momentum results. This case is very far from the comfort zone of the methods used in the wind turbine community.

1 Like
30

Does that mean I’ve just wasted a day doing this?

1 Like
31

Probably.
:))))))))))))))))))))))))))))

1 Like
33

I think there is benefit to being aware of these figures, but with variability wind and the array of kites available it may be hard to find data for anything other than a ballpark estimate.

I’m sure where I heard this but apparently the approximate power range is up to 30x minimum power?

If this is the case in Yo Yo mode or with any rotating AWES we could measure power over time. At X RPM the AWES produces an average of X amount of torque.

This is something more straightforward for “torque” AWES like Daisys or Superturbines, but for “pulling” AWES, there needs to be some standard of a R for Rotation.

For instance should the loop be a standard size or duration, that is difficult because each subsequent loop gets wider? Looking for suggestions

34

This would only be good for a standardised comparison of AWE designs. Changing the size and shape of the kite path would be a low hanging fruit for optimization. So in a future where AWE was in continuous operation at scale, one would certainly spend time optimizing these things.

35

Torque AWES like Daisy or SuperTurbine ™ can be assimilated to “drag” devices (flygens like Makani wings) or even conventional wind turbines, because the swept area does not move. So they are subject to the Betz limit (16/27).

In contrast pulling (yo-yo mode) AWES are subject to a limit of 4/27 of the swept area because it is going downwind at theoretically 1/3 wind speed, whether the use of crosswind or static (tethered-aligned) AWES.

In my last comment I wanted to show that a tethered-aligned AWES could go beyond the limit of 4/27 if the drag coefficient is higher than 1. I exposed a different conception where the swept area is the reference, in contrast to the usual reference of the kite area, at least for yo-yo mode. Parachutes with High drag coefficient and Parasails could lead to a better optimization of the swept area, so a better Power to space use ratio.

And we should keep in mind that the generation component of any AWES (as for a conventional wind turbine) always goes horizontal, being opposed to the lift component which goes vertical. It is the reason why crosswind kites flight at an average elevation angle of only about 30-35 degrees, so not too far from the horinzontal in order to mitigate cosine loss.

This is possible for well-sharpened rigid wings like the rigid blades of a gyroplane rotor. But as such a rotor scales up, the mass will quickly become much higher (squared-cubed scaling law for rigid things) than that of the parachute which “fills” the swept area. So, in yo-yo use, 30x power is not useful if we reason by swept area (here where the power available in the wind is limited to 4/27) as we should in my opinion.

1 Like
36

AWE lift power systems are also named as yo-yo or reel-out/reel-in or pumping mode systems.

Now what would become of the value of 4/27 if, instead of crosswind kites, tether-aligned devices like High drag coefficient parachutes (without their own lift) or Parasail-based Airborne Wind Energy Systems (with their own lift) are used to harvest the power available in the wind which is delimited by their projected area, knowing that very high coefficients (Cd) of 2.2 and more were reported?

For example if a tether-aligned (non-crosswind) parachute has a Cd of 3 (assuming it has no lift to simplify, or even a thrust coefficient (Tc) including a Cd of 3 and a lift coefficient (Cl) of about 1) “the power available in the wind” (in pumping mode, so with the quoted limit of 4/27) would be 3 times, so 12/27, is not it?

This is where the paradox becomes blinding: we will place in the “AWE lift power systems” category a tether-aligned parachute which only generates drag or, at most, a minimal part of lift compared to that of drag within the generated power.

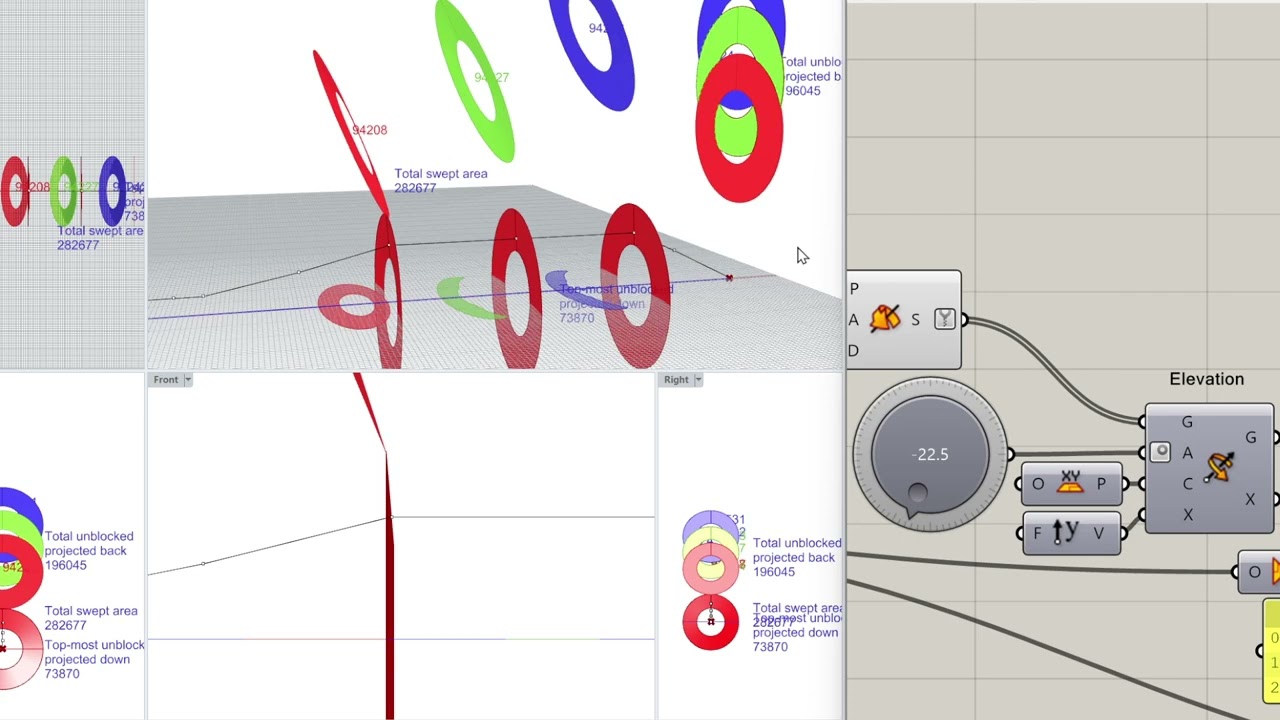
The explanation comes from the fact that the AWES mostly envisaged are crosswind AWES, generating lift to fly at several times the wind speed while sweeping a large area and producing great power relative to their respective kite area. This does not prevent the fact that for yo-yo mode, whatever the type of flight, the swept surface “retreats” and causes a loss of power compared to the Betz limit (16/27). But this loss or limit is measured on the swept area.

So, in yo-yo mode, a crosswind kite with a very high L/D ratio, will have a power potential equal to or less than that of a tether-aligned drag parachute whose area (filled with fabric) corresponds to the optimized swept area of said crosswind kite, and even very lower if our parachute has a very high Cd.

This raises a question: why persist in wanting to use a very efficient (high L/D ratio) glider in relation to its kite area, to ultimately sweep less area than a parachute with equal masses, and that with a lower efficiency per swept area unity?

It is believed that a small kite going faster will take up less space: this is without taking into account the length of the tether, and the take of fast crosswind figures requiring more spacing between unities, and diminishing the Power to space use ratio.

37

I think this is easy. Compare the swept area required and then design a system for ground handling, launch, land, control. All of these are very difficult.

Eg. compare to a Vestas 4 MW wind turbine. Swept area is maybe 15k sqm. That produces maybe power according to Betz 0.5 \times \frac{16}{27}. If you assume a parachute in bounding mode produces power 0.5 \times \frac{4}{27} You need kites of 60k sqm to produce the same power.

A circular parachute would have 280 m diameter in that size.

Even simplifying that to 4 kites of 15k sqm does not really help much.

And how do you deal with changing wind speeds? having no ground speed tales away one main method to control tether tension.

And, how long could that tether be without falling on the ground, in low winds.

I could provide the detailed formulas, but I just dont think its worth the effort. An argument like if rigid wings dont work, then this is the better option changes nothing. The idea must stand on its own legs

38

Assuming the weight of a parachute could be 0.1 kg/m², the total weight would be 6 tons. This would be approximately the mass of a 4 MW rigid glider with a high L/D ratio, which would have a very high cut-in wind speed requiring frequent landings and takeoffs, if of course it completed flights without too much risks of crashes.

A parachute has a much lower wing loading per unit area, which allows it to stay aloft even in light winds.

This would reduce the total surface area (for 4 MW) from 60,000 m² to 20,000 m², which would start to be acceptable with a train of many stacked units going high enough to exploit the truly high altitude winds. And very high coefficients (Cd) of 2.2 and more were reported, as well as a very High drag coefficient (Cd) of 2.727 for a parasail, and lift force (as for any parasails), tested and reported on
Sea recovery system for small UAV | NTU Singapore.

Zhonglu High Altitude Wind Power System began flying trains of parachutes while generating some power (22 kW?).

39

Pierre,

If we consider airborne wind energy systems to be akin to gears, with drag-based systems resembling high torque, low RPM gears due to their reliance on wind resistance, and lift-based systems acting like high RPM, low torque gears because of their emphasis on movement and lift, how might this perspective influence our approach to optimizing the design and efficiency of these energy harvesting systems?

I recently had a conversation with Dan Tracy, who kayaks with kites, and he highlighted the remarkable power generated by a looping foil compared to a static one, especially given the same sail area. Do you think there’s a difference in power output between these two setups? Furthermore, considering the looping motion, wouldn’t certain parts of the loop produce more lift, while others generate more drag, depending on the wing’s orientation at various points in its rotation?

40

Of course yes, since I tested Low radius loop : the power is multiplied by about 7-8 times. It is a little more in surge and a little less in average for figure-eight I also tested with the same kite. Now if a parasail with a Cd of 3 is achievable (and a correct Cl to obtain a correct elevation angle of about 30 degrees), the loop power would be only 2 or 3 times more, for far more control issues, and perhaps more wear. So further study and testing may be worth it.

41

I will get you the yo yo/ spiral data ASAP. The company I buy motor controllers from just released a really fancy display unit that gives all sorts of data. Perhaps we can collaborate to devise an experiment that could correspond to your methods and dataset.

It’s my opinion that any adept system should be able to do both… When machine learning takes control of the flying, there may be situations where both regimes are warranted. The point is not to inhibit the kite in any way. The main goal is to reduce lines from grazing against one another, reduce wear, and improve efficiency by avoiding twists.

So Figure 8 vs Loop is not quite the hill I will die on, rather the mountain that constitutes both.