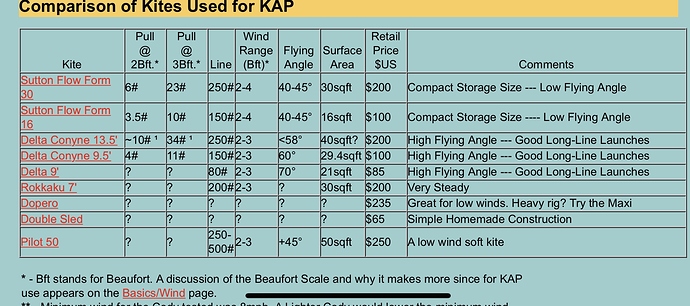
I liked this table a lot.
Also the SSSL 3m2 that I have been flying is not on the list (not a good kite for KAP), but it flies at >67 degrees and pulls ~5-7 kg in 5 m/s wind. That would be 11-15 lbs in beufort 3 I guess. Flying so high puts it in a separate league for soft kites, and it is cheap and packs very small
Both so high pull and flying angle look to do an exceptional combination. This kite would almost be suitable for a non crosswind AWE yoyo system.
Its true. Though no depower at the moment. The kite collapses quite easily for full depower, but collapse is kind of random wrt handling
What would be the flying angle (from 67 degrees in static flight) during reel-out phase?
Assuming wind speed is 5 m/s, pull in static flight is 60 N, reel-out speed = 5/3 m/s if possible, the pull becoming 26.66 N as the apparent wind becomes 3.33 m/s.
Note: the optimal 1/3 reel-out speed can be difficult to achieve due to the high flying angle, but I can be wrong.
60 N pull leads to lift = 55.4 N and drag = 23.08 N, assuming L/D ratio = 2.4. During reel-out phase the resulting pull of 26.66 N leads to 24.61 N for the lift, assuming the drag value doesn’t change, leading to a L/D ratio of 1.06, roughly 1, so a flying angle of about 45 degrees, and the power of this 3 m² kite would be 26.66 x 3.33 x 4/9 = 39.4 W during reel-out phase, 13.9 W due to cosine-cubed law with 45° elevation (flying) angle.
26.66 N is the resulting pull as the reel-out speed is 1/3, so the apparent wind 2/3 of 5 m/s, lowering the force and power by 4/9.
The problem with producing upwards I touched upon in the Laddermill thread. My conclusion is that energy is produced mostly in downwind direction. The kite would need to loop downwind for real energy production
The intuitive reason is that once you release tether fron the spool/winch, a kite flyibg at zenith will immediately lose most of its power
I experimented a soft kite making small loops on Low radius loop - #7 by PierreB, the force being about 6 times the kite area (power harvesting factor), that is a value close to the maximum value which would be achieved by using a kite of which its area is as large as the swept area by the loop.
The downwind component is the same by using both static (the present lifting kite or Laddermill) and crosswind (small loops or large lemniscates) kites.
Sir,
Can you please explain how you calculated the power from the given kite size? I have a 12m2 Airrush lithium kite and the wind speed ranges from 4-6m/s. Please help me in calculative the approx. power.
Thank you.
Hi. Welcome to the forum!
You can estimate the power of such a kite in this way: we’ll start by assuming that the kite and tethers (at a given length, if you add length performance will deteriorate) have a certain glide number (lift to drag ratio) and a certain maximum pull depending on airspeed relative to the kite. Also you may assume as a start that the mass is zero.
To find the pull, measure the lift of the kite standing still above your head, and at the same time measure the windspeed at the kite. You may deduce the K in the relation between kite force and airflow at the kite:
F = K v^2
Next, to deduce the glide ratio, measure the angle between vertical and the kite, also at rest above your head. The glide ratio is G = \frac{1}{\arctan{\alpha}}
The power in a certain wind speed has a upper bound:
P = \frac{K G^2 w^3}{3}
You may read a lot more about this in certain papers and the AWE book. But this should be a good start if you want to approach this from a practical point of view.
As a starting point, I would assume the values for such a kite is K \approx 3 and G \approx 4. Just a wild guess. So 2000 W in 5 m/s wind.
(Note I fixed on of the formulas.)
Welcome @Roystan,
Before trying to reply to your question, I put a link about your activity as searcher for AWES.
https://www.daijiworld.com/news/newsDisplay.aspx?newsID=386189.
I think the current topic is about some elements of efficiency of a static kite.
But probably you use crosswind path and in yoyo mode, taking far more power by using figure-eight, leading to a larger swept area and a higher apparent wind. A basic paper about calculation is
Assuming wind speed is 5 m/s, cubed wind speed is 125, air density is 1.2, lift-to-drag ratio is 4, lift coefficient is 1, elevation angle is 30° leading to cosine = 0.866 then cosine cubed = 0.65. I use the equation (2) from the paper, adding cosine loss which is mentioned later in the paper.
(1.2) (2/27) (12) (125) (4²) (0.65) = 1386 W during reel-out generation phase. The time and the power consumption during reel-in phase lead to an average of about 600 W.
A similar result can be obtained by multiplying the force (equation 1 from the paper) with reel-out speed which is 1/3 of 5, so 1.66. The reel-out speed is the speed of the unwinding speed of the rope which is seen as optimal when it is 1/3 wind speed. Cosine squared is 0.75.
(1/2) (1.2) (12) (5²) (4²) (0.75) = 2160 N. Then (2160) (1.66666) (4/9) (0.866) = 1386 W.
I precise 4/9 is due to the squared loss of force due to the 1/3 loss of apparent wind speed during reel-out phase.
Other losses are not mentioned and comprise losses by transmission of irregular power as the power varies within the flight window, by cosine due to the gravity (see the paper)… So one can expect an average of 300 or 400 W.
The power can be measured by knowing the force (using a peson) X the reel-out speed.
@PierreB thanks for your answers. I had done my UG project work in this field without realising these calculations, now I’m researching on this area as a full time research scholar. I’ll look into the paper you have suggested. Thanks!
@tallakt thanks.
I added a note about having calcuclated wrong putting my result up to 600 W more aligned with @PierreB’s value of 1386 W.
For power generation, you would normally want to increase the lift-to-drag ratio and also perhaps the windspeed to generate “serious” energy for such a large kite. If you need to generate energy in as low windspeeds as 4-6 m/s an effective (high G) kite and high power to mass seems the way forward.
Below is a sketch:
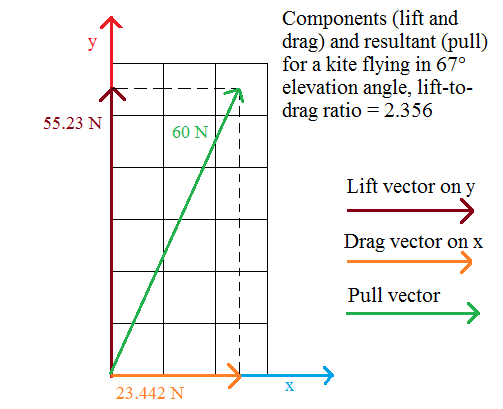
I believe I had taken the cosine loss and the 4/9 factor (loss of force by resulting apparent wind) once too often. And also the theoretical optimal reel-out speed for a wind speed of 5 m/s is 1.66 m/s. So 26.66 X 1.66 = 44.4 W. That said @tallakt’s remarks below are relevant:
I would add the downwind direction is also more in the center of the flight window where the efficiency is higher.
5 posts were split to a new topic: Using a kite lifter as a low aspect ratio power kite