A simple website to calculate the powers (exponents) of numbers (bases):
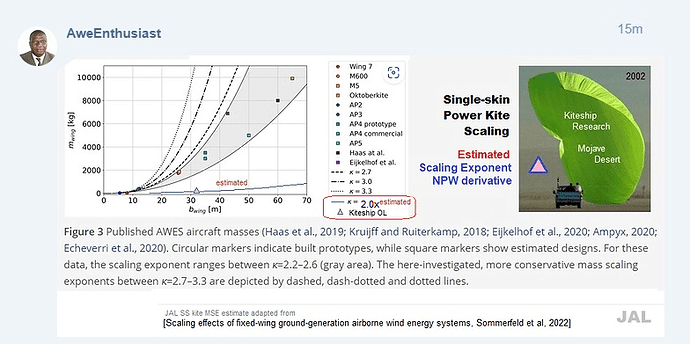
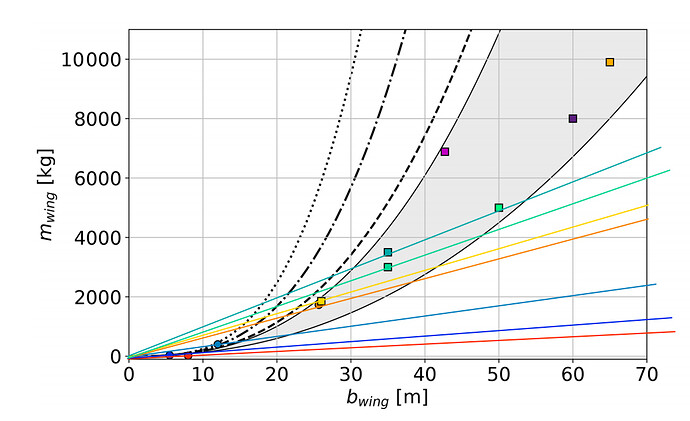
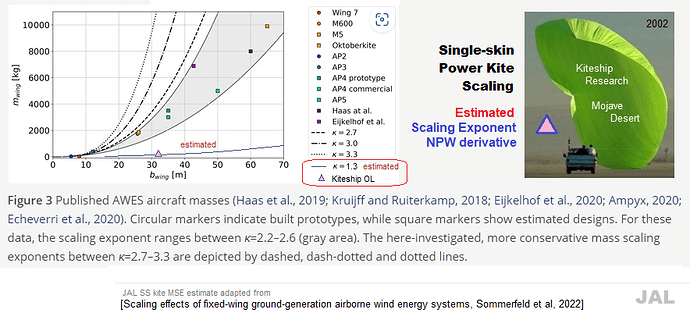
The paper is about rigid kites, so the more or less cube (cubed mass m³ following the volume) scaling law applies: (exponent) K = 2.7, or K = 3, or K = 3.3.
If the base = 10, we obtain about 501 with K = 2.7; then 1000 with K = 3; then about 1995 with K = 3.3. If the base = 2, we obtain respectively about 6.5; then 8; then about 9.85.
For flexible kites (by the numbers of the linked publication the mass increases a little more than the area, this increase slightly increasing as the wing becomes larger; and also take into account that the examples given in the publication may not be fully representative), an approximately square (squared mass m² following the area) scaling law applies, leading to K value of about 2.1-2.3 by my rough estimation, not as a result of the calculation of the numbers in the publication linked above.
If the base = 10, we obtain about 126 with K = 2.1, and about 199 with K = 2.3.
If the base is 2, we obtain respectively about 4.29 and about 4.92.
K value of 1.3 as stated on the comment above, would lead to a smaller increase in mass than the increase in area, which does not seem correct, compared to the quasi cubic K of 2.7, 3, and 3.3. Indeed if the base is 10, we obtain about only 19.95, and if the base = 2, we obtain about only 2.46, while with the exponent K = 2 we obtain respectively 100 and 4.
It is the reason why I consider an exponent slightly higher than 2 for flexible kites.
Note that there is a huge difference between K = 2.3 (the high end of my estimates by a ladle, for soft kites), and K = 2.7 (the low end of the estimates for a rigid kite).