(NOTE: I edited this post after due to some calculation errors I made originally. I left some notes in italic writing, otherwise the text remains)
I wanted to make a stab at figuring out the scaling of the structures that keep the rotating turbine shaft at a certain diameter
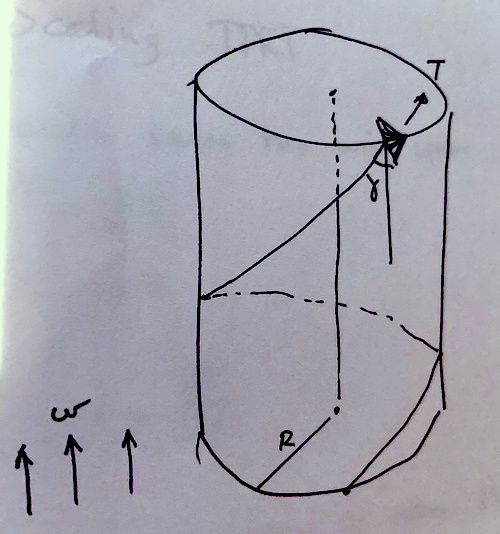
My thinking starts with a single kite, the wind blowing directly from below (I am not looking into the power generation much here). The tether is kept in shape on the outside of a cylinder shape by some unknown force (the fine grid of carbon fiber rods in practice, or some inflated structure).
This is a simplified structure for analysis.
What do we know? Well this is a drag mode AWE rig, so the angle \gamma is predetermined when running at optimal production (something like slowing down the kite one third). I won’t go into further details just here. The cylinder radius is R. The tether tension is constant T. The length of the tether is l. All of these are assumed to be constant.
The force required to keep the tether at a cylindrical shape may be calculated by splitting the tether into infinitesimal sections then using Newtons equations to calculate radial force balance. I found that:
\frac{d C}{d s} = \frac{T}{R} \sin^2{\gamma}
C is the sum of forces applied along the tether outwards from the center of rotation, the free variable s being along the tether length (also I am skipping how I came to this equation for brevity).
At this point we decide to scale the wingspan of the kite by a factor x. The produced power scales with the area of the wing, thus \tilde{P} = x^2 P (I am using tilde to mark the scaled power, and P without tilde for the non-scaled power). We will scale the whole rig also by x, leaving us with \tilde{R} = x R, \tilde{l} = x l, \tilde{T} = x^2 T.
\frac{d \tilde{C}}{d s} = x \frac{T}{R} \sin^2{\gamma}
Next we will assume that the structure keeping the rotary shaft at a certain diameter is built from carbon rods. We will maintain the same number of these structures (rings). As both the distance between rings and the tension of the tether has increased, the pressure that must be withheld is scaled by x^2 (one x for scaling of \frac{d \tilde{C}}{d s}, one x for scaling of the distance between the rings). Also the size of the rings themselves must increase by x.
To figure out the new thickness of the rods, we will consider the buckling load of the rods. The buckling load is given by
F = n \pi^2 \frac{E I}{L^2}
Having E as a constant dependent on rod material, L being the length of the rods, and I being the moment of inertia of the rod. As the rods are cylinders, I = \frac{1}{2} \pi \rho L r^4. r is the radius of the rod, \rho is the density of the rod material. Thus
F = \frac{n \pi^3 E \rho r^4}{2 L}
We’ll scale the radius of the rods by a factor \tilde{r} = y r. The length \tilde{L} = x L. Last, we need:
\tilde{F} = x^2 F
\frac{n \pi^3 E \rho y^4 r^4}{2 x L} = x^2 \frac{n \pi^3 E \rho r^4}{2 L}
y^4 = x^3
y = x^\frac{3}{4}
Thus the mass of each rod will scale by
\tilde{m} = (x L) \pi (y r)^2 = x^{2.5} m
We can conclude that the weight of the supporting structure will scale by scale to the power of 2.5. This is not really bad considering that the tether tension T (almost equal to the lift) scaled by a power of 2. We could set up an equation comparing the scaled and non-scaled ratio of support structure mass to tether tension:
\frac{\tilde{m}}{\tilde{T}} = x^{\frac{1}{2}} \frac{m}{T}
All in all looking like something that will probably not become a serious issue for a long [scaling-] time yet. NOTE: This conclusion is probably wrong. This is a serious scaling issue. The relative mass of the shaft increases by x^{\frac{1}{2}} which is not really a good thing
Now some final comments as to why rotating rigs will not go high-altitude withtou futher innovation: Compared to Yoyo, the whole tether is moving. This increases tether drag by a factor of 4. Next, you need to split the tether into n thinner tethers in order to get a geometry suitable for torsional transfer (assuming there are rings or other supports). This will increase the tether drag by \sqrt{n}. For n = 6 the increase in drag is by a factor of 2.44 compared to a single tether rig.
I’m not saying rotational is not worthwhile, I’m just saying that if it works, it probably will work at somewhat lower altitudes. Personally I still think this concept may be worthwhile. NOTE: Again, the conclusion is not as clear anymore