I am spilling the details of my “Superturbine” that I have been working on lately, also in cooperation with @Rodread and Oliver Tulloch. It will be presented at AWEC21 in Milan in June.
Please find the complete detailed description here [44 pages].
I would like to describe some high level findings.
The Pyramid is/has:
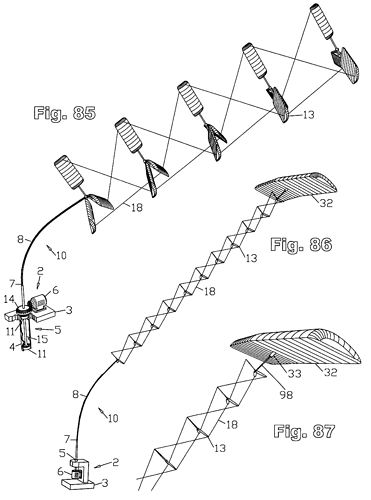
- a three kite AWE architecture
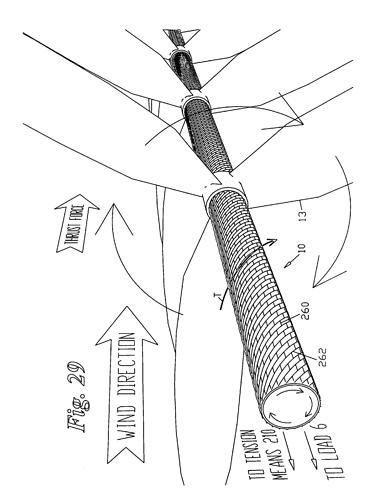
- a TRPT shaft (rotary moment based power transfer) with three tethers
- a triangular bridle between the kites
- a rigid cartwheel at the ground
- the cartwheel raised slightly by a small tower
- active kite control to ensure constant tether tension and elevation control by rolling the kites
- a sane way to launch and land (presumably)
- no rigid elements in the shaft or otherwise airborne
In addition to all this, the Pyramid is a simple platform to learn more about TRPT architectures, as it’s “the simplest possible thing” with that starting point.
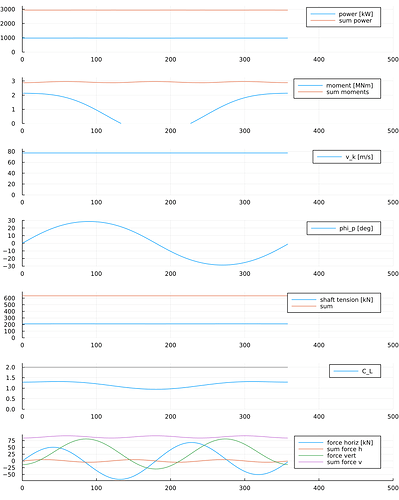
In the document we see that the moment bearing capability of a shaft may be described by the \Lambda value, representing the moment transferred in the shaft divided by [per] tension and kite looping radius. Any TRPT shaft may be assigned a \Lambda value even if it contains rigid elements, multiple sections etc.
The maximum \Lambda value for these kinds of simple shaft that we are looking at here with tether length l, ground radius r_0 and kite radius r_1 is given by
\hat \Lambda \approx \frac{r_0}{\sqrt{l^2 -r_0^2 - r_1^2}}
The maximum power of the rig is generated when the \Lambda value approaches
\Lambda_{opt} \approx \frac{1}{2 \frac{C_L}{C_D}}
Note that C_D in this respect contains drag of both kite and tether.
We also show that the TRPT shaft, when scaled in every dimension by a factor x, can transmit power scaled by x^2. This will exactly match the power production capability of a kite scaled in wingspan by x and in wing area and power output x^2. So the match between the two could scale “forever”.
Then there is a description of a control algorithm to keep tether tension constant, and to provide an elevation angle.
Then there is a simulator which is, if I dare say, quite decent, open sourced at https://github.com/tallakt/TRPTSim
There are mentions of the trouser mod and umbrella mod to reduce tether drag at the expense of reduced \Lambda for the trousers mod, and vice versa for the umbrella mod. Both without requiring any rigid airborne elements.
Even more then, there is a discussion of the feasibility of the architecture given the inherent drag of the tether along with the fact that to get the correct \Lambda values with long tethers, the system drag must be kept low. This is shown to be ok within a certain design window. Also, introducting the tether aspect ratio \varrho = \frac{l}{d} with l being tether length and d being the diameter, the design window is plotted in a nondimensional plot valid for any scale of the design.
In short - this is possible. Until square - cube mass scaling gets the best of us.
Enjoy!



 .
.