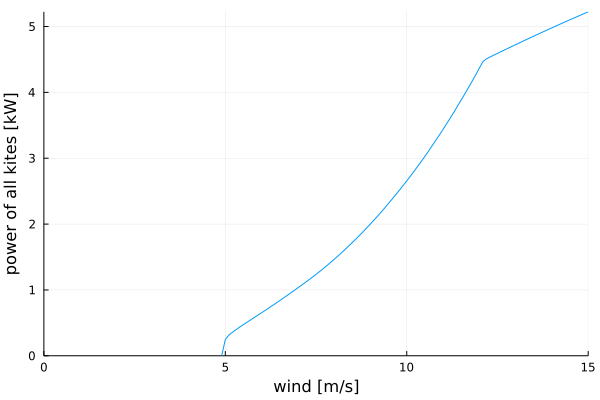
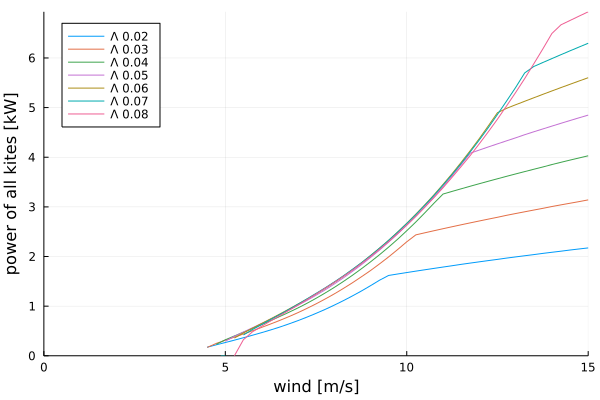
I am here considering using a Durafly Excalibur for testing rotary launch for “The Pyramid”. The launch looks something like this:
More info about the pyramid in this thread:
And the Excalibur looks like this:

It has:
- Wingspan b: 1.6 m
- Chord c: approx 0.12 m
- Weight m: approx 1.2 kg
- Distance CG to tether attachment below fuselage d: approx 0.035 m
- Wing area S: approx 0.19 m2
The triangular bridle between the three “plites” is assumed to have a radius R which will be 1.5x wingspan for now at 2.4 m.
Note this plane can me flown without the front prop.
Summary
The roll control of the Excalibur is feasible for the proposed launch sequence and you can choose to have inherent roll stability by selecting an initial roll angle for the “plite” according to the other system parameters. The design should scale without change in feasiblity.
Assumed roll torque authority
Lets assume the maximum C_{L, max} \approx 1.2. If we have set ailerons to provide max lift on one side and zero on the other, an approximate rolling moment would be
\tau_{\delta, max} = \frac{1}{2} \rho C_{L,max} v^2 \frac{1}{2} S \, \cdot \, \frac{1}{4} b
\tau_{\delta, max} = \frac{1}{16} \rho C_{L,max} v^2 S b
v is the kite flying speed, \rho = 1.225 is air density.
The specific value of moment per speed squared is
\frac{\tau_{\delta, max}}{v^2} = 0.027 \, \mathrm{Nm}
Rolling moment of the wing
So the kite is flying in circles in the plane of rotation with radius R. The inner half of the wing will experience lower airspeed than the outer half, so it will provide lesser lift and thus a rolling moment.
For simplicity we will assume the chord constant and the lift over the wind evenly distributed. This gives a good rough estimate of the moment involved. Later a CFD analysis or practical testing may give a more accurate estimate.
Also, the kite is flying at a roll angle to the plane of rotation which is \phi.
We disregard any effect of gravity and wind here.
The torque of the wing may be expressed as an integral
\tau_w = \int_{-b/2}^{b/2} \frac{1}{2} \rho \left(v \frac{\left(R + x \cos \phi \right)}{R} \right)^2 C_L c x \, \mathrm dx
\tau_w = \frac{\rho v^2 C_L c b^3 \cos \phi}{12 R}
The value of this moment per speed squared, at C_L = 0.6 and \phi = 0 is
\frac{\tau_w}{v^2} = 0.0125 \, \mathrm{Nm}
So for \phi = 0 the moment generated by the wing is much less than aileron control authority.
Tether moment of the wing
The tether moment is due to “centrifugal force” and at the same time the tether is attached (for practical purposes) at the bottom of the fuselage. This will create a moment
\tau_T = -m \frac{v^2}{R} \, \cdot \, d \cos \phi
The value of this moment per speed squared, at \phi = 0 is
\frac{\tau_T}{v^2} = -0.013 \, \mathrm{Nm}
This moment is also less than the supposed control authority of the ailerons, by a factor of approximately 2.
All moments
The sum of moments on the “plite” is
\tau = \tau_\delta + \tau_w + \tau_T
The range of \tau_\delta [aileron roll moment] is the largest of the three by far. The other two mostly cancel each other out in this configuration. We should be able to control the roll of the kite in this phase by feedback control on the ailerons.
But, both \tau_w and \tau_T both depend on \cos \phi, so \frac{\tau_w}{\tau_T} = const. For roll control to be stable without active control on the ailerons (\tau_\delta = const)), we require that
\frac{\partial \tau}{\partial \phi} < 0
This translates to (solving the derivative)
-\frac{\sin \phi \left(\rho C_L c b^3 - 12 m d\right)}{12 R} < 0
\sin \phi \left(\rho C_L c b^3 - 12 m d\right) > 0
This means that depending on the value inside the parenthesis, we can select a roll angle to ensure that the roll angle is stable without active control.
For this particular design we may choose any negative \phi, for example \phi = -30^\circ. We must use active aileron control to get to that roll angle, but after that, the “plite” should be stable in roll without any further adjustments to the ailerons.
An interesting observation is that we can impact the roll stability of the “plite” by adjusting the system parameters, most easily d, distance from CG to tether attachment point.
Edit: From this analysis it seems maybe we want the d to be rather large so that \phi is negative. This gives ut the benefit of wing lift pointing outwards, tightening the triangular bridle between the plites
Scaling
We will see what happens to a version of the demonstrator where all dimensions are scaled by a factor x. The mass is assumed to scale by x^3.
\tau_x = \frac{\rho v^2 C_L \left( x c\right) \left(x b \right)^3 \cos \phi}{12 \left(x R \right)} - \left(x^3 m \right) \frac{v^2}{\left(x R\right)} \left(x d \right) \cos \phi
\tau_x = x^3 \left( \frac{\rho v^2 C_L c b^3 \cos \phi}{12 R } - m \frac{v^2}{R} d \cos \phi \right)
The moment scales by x^3 but the ratio \frac{\tau_{w,x}}{\tau_{T,x}} does not change with scale. So we can conclude that at any scale, the launch scheme should still work fine.