Flettner balloon and VAWT side by side

[PierreB]

It can be interesting to simplify the AWES when all elements are rotating, working together, and by using rope drive transmission, being stationary. Stacking could also be easier.

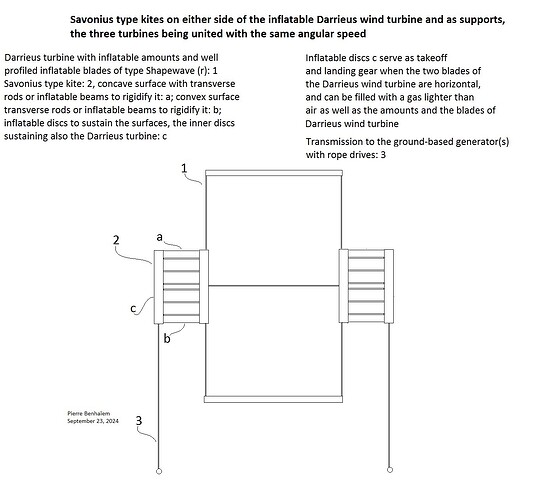
Magenn proposed a sort of balloon surrounded with blades of type Savonius. In this conception the Magnus effect is operating at the tip of said blades, and not at the level of the balloon which “eats” the area concerned by both Magnus effect and the swept area for power generation. And this type of AWES using Savonius blades are difficult to achieve, while being not efficient.

I experimented other configurations such like a Sharp rotor within a VAWT (Darrieus-like). Even with strong wings above 10 m/s, the Sharp rotor did not generate any lift, likely due to interference between both rotors.

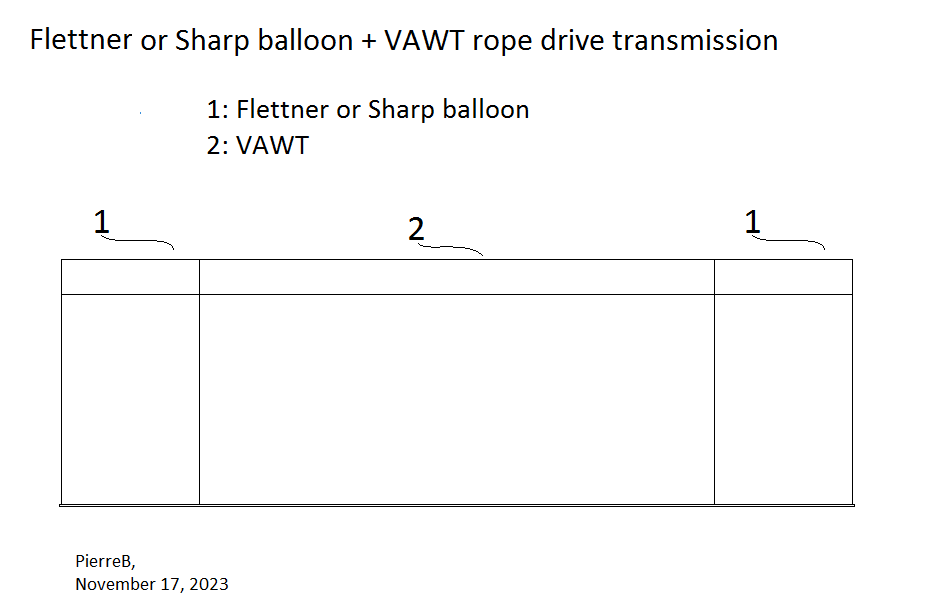
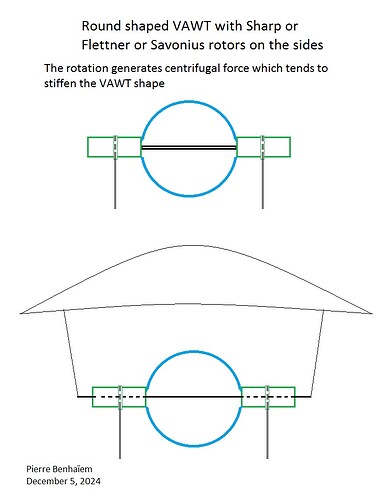
So a side by side configuration is studied. But the maneuver (take-off, landing, then stacking unities close each other) would be far easier if all elements were aligned and of same diameter.

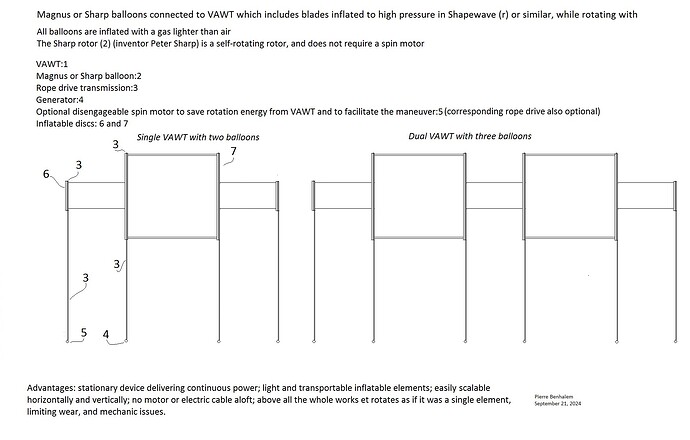
A Flettner balloon is very easy to build and can support the blades of VAWT (Darrieus-like) which can be made by using shapewave® technology. The spin ratio of the Flettner balloon should not be too high, being about 1-1.5. As we know, the power consumption increases by the cube of the tangential speed and would be too high with spin ratio above these values. So the TSR of VAWT should also not be too high, being the same as the spin ratio of the Flettner balloon, leading to a same diameter for all elements.

VAWT Darrieus-like showing low TSR (see Figures 14, 15, 21, and 22) but also high solidity, are studied on:

528418.pdf

TSR = 1 or just above with a coefficient of performance of 0.3-0.4 far above that of any Savonius-like rotor.

The high solidity is perhaps not a big issue since for VAWT, the section being the same for the whole length of the blade, unlike the twisted blades for large HAWT, allowing also them to be light by being inflatable and now rigid enough thanks to new inflation technologies.

I put again a sketch as an example:

A Flettner balloon is far easier to build and its power consumption is low for a spin ratio of 1, and acceptable for a spin ratio of 1.5.

See the formula (which I put in full letters) in the last page of the pdf of Experiments on a Flettner rotor at critical and supercritical Reynolds numbers : 0.007 x span x diameter x 3.14 x tangential wind speed³ x air density/2.

[PierreB]

An example of an unity, then a farm of unities, then a farm of farms, by using the same two elements alternating, and stackable horizontally and vertically:

[gordon_sp]

The problem with multiple parallel cable drives is that there is no way to ensure that the tension is the same in all of them. If the tension in any cable drive is too low, then it might slip or entangle.

[PierreB]

Indeed this is an issue. And also any rope drive could possibly escape from the balloon.

This design was intended to see how balloons and VAWT could be mixed in order to provide lift by Magnus effect.

A yo-yo (reeling, like Omnidea balloon, the VAWT of type Darrieus replacing spin motors) version could also perhaps be studied:

[PierreB]

Some experiences last days, using the same 0.52 m x 0.3 m VAWT. The VAWT power is used to spin the 0.2 m diameter bottle(s) which replace Sharp rotors.

Bottle kite:

Rpm 500 in the first part of the video, rpm 1000 near the end, wind speed 8-14 m/s:

bottle kite

Double bottle kite:

Rpm 350, wind speed 10-16 m/s:

double bottle kite

[dougselsam]

Great experiment Pierre. Something never done before, requiring no funding, no interns, no new test facility in Ireland, no renting of office space, no director of human resources, no go-fu**-yourself - er, um, I mean “GoFundMe” effort… I don’t see how you could have done this without a few scientific papers, an ample staff, and a dedicated industrial facility! And by the way, I thought you guys were all out of empty space over there in Europe - looks like you have plenty! Looks like a great place to live!

[PierreB]

Thank you for your words Doug. I would add that I will not issue a triumphant press release.

Indeed a VAWT of dimensions equivalent to the Omnidea balloon should be juxtaposed in order to replace the spin motors, taking into account a very high power consumption (much more than the rigid cylinder experienced in this publication).

[dougselsam]

One thing i noticed: the bottles are pretty short, and if longer, would have a higher aspect ratio, (wingspan-to-chord ratio), which should give more lift, and a better lift-to-drag ratio.

[PierreB]

I wanted to experiment with something whose diameter (0.2 m) is close to the height of the VAWT (0.3 m) to have the maximum possible peripheral (tangential) speed and therefore rotational energy consumption (which increases to the cube of the tangential speed). I didn’t have anything else on hand at the moment.

[dougselsam]

Well of course I know you already are aware of this, in general, and I assumed you just used what was on hand and ready for use, which is better than waiting for the perfect bottle, but I just thought I’d mention that longer bottles should give more lift.

[PierreB]

@dougselsam

longer bottles should give more lift

It is true. I have bottles with a higher aspect ratio, but the diameter is only 0.1 m. The TSR of my old and patched up VAWT is barely above 1. That means the TSR (or spin ratio) of the bottle would be only 1/3. This is not a good value for an efficient Magnus effect.

I tested thinner bottles with a propeller connected via a bevel gear. The TSR of the propeller was 5 or 6 with the bottles of which the TSR (or spin ratio) was about 1. There was no perceptible lift, unlike the present VAWT with one 0.2 m diameter bottle (spin ratio until 2/3) but also with a far stronger wind.

I reproduce the video: