Vertical trajectory for yo-yo AWES?

Engineering Flight Control
1

Both chapter 12 and chapter 13 (see also the comment and reply section) in the second AWEbook describe a vertical trajectory for Magnus Effect-Based AWES in yo-yo mode.

I think the same with a classical kite could allow to use a far larger kite than by flying in figure-eight thanks to the absence of turns because the kite rises by its leading edge and descends by its trailing edge. That can lead to a maximization of the space and land use which are delimited by the tether length as radius by considering all wind directions. So the kite span could be equivalent to the tether length: 900 m span kite for 1000 m tether length as extreme value, leading to roughly 150 MW in average before some losses, with a L/D ratio of 4 and 10 m/s wind speed.

In proportions it is like a paraglider with its lines. Of course relatively higher tether length can be used. An advantage could be the simplicity of the flight control and its management, that at any scales.

Today I experimented a vertical trajectory with a four line 4 m² kite, alternating power ascending and depower descending phases. I noted that both went in a similar speed. And the depower can be complete with appropriate maneuvers. This bodes well for the yo-yo reel-in phase.

A low quality video shows these tests, and below another video shows the same between 8:30 and 8:42.


2

It is true and may be ute ultimate expression of super short tether AWE.

You could probably make a kite to fly up and down well (without resorting to making the kite a ÂŤbagÂť). Going down should make less/no power.

There is a slight issue with flying up/down, and I would rather go right/left. This is to deal with gravity. When going up, you can’t easily point the lift force upwards to compensate for gravity. Doing this will change the angle of attack. If you are flying left/right, this is just a matter of rolling slightly.

Second thought: is this better than a rotating rig with three kites? It takes a while to accellerate the kite for every cycle. With a rotating network the cycles could be longer for pumping, or continuous with drag mode power takeoff.

3

You raise relevant points but not without possible answers for what I think.

Gravity is a disadvantage during the climb (reel-out phase), but an advantage during the descent (reel-in phase), considering vertical paths.

Both chapter 12 and chapter 13 mention quite vertical trajectories by taking account of reel-out and reel-in phases. The tether reel-out speed results from the increasing of the elevation angle of said tether. During reel-out phase the kite undergoes both the same real and apparent winds in a way that the angle of attack stays the same for what I think.

Yes, but the kinetic energy of the kite is used when the kite ends its raising where the power zone decreases by going towards the zenith. As a result the loss of time to accelerate is compensated by achieving a higher altitude and elevation angle.

Yes, but turns are needed and require place, preventing the kite scaling up beyond some point, unless it is divided into smaller unities whose the management can be quite difficult.

Or even only one kite as for Low radius loop - #7 by PierreB.
It depends, among other things, on how far the kite can scale. The purpose is the same: maximizing the space. For what I think the figure-eight does not allow it enough due to flight requirement.

4

This works ok with a lightweight kite. e.g. rev or single skin.
The bottom transition (from flying Backwards to going Up again) is where I see a problem for scaling.
OK, you’ll be reeling in when falling so, You’ll not likely have to re establish the flow direction over the wing… That’s ok-ish
but you do have to decelerate the fall and accelerate up from the bottom again where the winds are lower. Power for an apparent wind speed boost will be coming from the yo-yo.
There’s a lot of control needed in this style of flying.Best if all the controls are on the ground.

You’d want the control winding to be closer together and use a longer stroke to span distance than hinted in this old vid…

Yeah that old model was really complex looking.

I tested an arch kite made from 4 windsurf sails a few times. On the last go, it was windy. Having previously flown smoothly and cleanly. This time it galloped and thrashed and ripped. That was some fierce vertical stroke pumping.

5

This seems to be a bit confuse I think. A nice rendering is not a conceptual explanation. About:

In the bottom of the path, the winds are yet good enough. My 4 m² soft ram wing on the video ascended at full speed immediately after the controlled fall. The explain is simple: its weight is negligible compared to the pull force. Even the kinetic energy due to the fall is low compared to the pull. As an example the weight of my 4 m² kite is 8 N (0.8 kg). Assuming the speed is 20 m/s for the climb as for the descent, the kinetic energy is 192 J, while the pull force is 960 N. The weight/pull ratio is about the same regardless of the size of the kite, or would increase slowly until a critical (?) value which can lead to a huge kite. At worst, a few seconds will be spent on really huge kites, and recovered at the end of the trajectory thanks to the this this time positive kinetic energy during the climb. So I do not see any real problem for scaling in any size. On the contrary, I conceive of this type of trajectory as a means of maximizing the space used, unlike to what results from the figure-eight. And the vertical path, said also 2D (3D being for figure-eight), can also allow the implementation of really small and yet powerful AWES, for example by using a (1.5 kW) 9 m span kite for 33 m tether length.

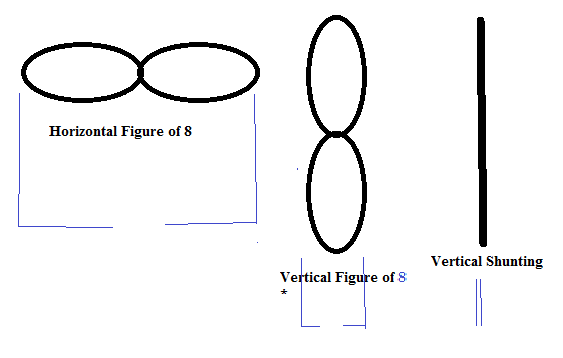
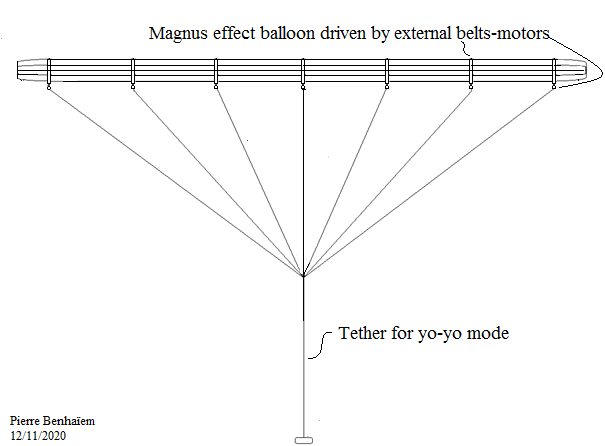
For general information about vertical path as a start reading carefully chapter 12 and chapter 13, particularly the fig.12. 23. on the page 300 of the chapter 12, showing the vertical trajectory and the swept area that is delimited by the Magnus balloon, and also the table 12.3 on the page 297 where the dimensions of the balloon and its mass are mentioned, respectively 80 m span and 50 tons. Certainly it is a balloon inflated with helium, but the mass of inertia plays a role during transitions, and seems to be taken into account by the author.

Concerning the fig.12. 23, the low position is at about 50 m from the ground, so not too close; and the top position is at 220 m from the ground. As the horizontal distance is about 200 m (do not forget we speak about a vertical trajectory), the elevation angle of the low position is about 14°. The elevation angle of the top position is about 47°, leading to a tether length of 293 m, then 87 m for a reel-out/in phase.

If we extrapolate towards my initial example of a 900 m kite span, the tether length should be about 3299 m, comprising the 980 m for each reel-out/in phase. It is a higher value that the value I initially mentioned, but still low compared to the kite span. This higher value results from the requirement to go far from the winches in order to optimize the crosswind flight in a similar way as the papers indicate.

The mass of a single skin kite is far lower than that of a Magnus balloon, and its weight is two orders of magnitude lesser than other lift and drag forces. So the bottom transition may not be insurmountable.

6

Thanks Pierre.
It’s a bit early days to be scaling to 900m . . . Slightly ambitious.
Chapter 12 test results on page 291 fig 12.14 Net output power
drum roll
0.0099055W That’s a lot of numbers and zeros …
Just not all on the right side of that pesky point thing.

7

If you prefer only (1.5 MW) 90 m span for only 330 m tether length, comprising the 98 m for each reel-out/in phase, or even (1.5 kW) 9 m span for 33 m tether length comprising 10 m reeling. As I indicated several times the tether length should not be too high compared to the kite span or the swept area. Even Makani 600 kW is too small compared to its space use. And Google and others will not give a second chance so easily. So a credible method allowing scaling NOW is required.
Other than that, I think I can do without your remarks on figure 12.14, remarks which has little to do with the subject. The only thing to note about this figure is the substantially equal duration of the power and recovery phases which could confirm a rate of climb equal to that of the descent that I mentioned for a classical kite it is true.

8

True, but the path can become vertical by using yo-yo (reeling) mode. I think the use of a vertical path in yo-yo mode leads to some potential advantages: the implementation of a far larger kite thanks to the absence of turns (which is also possible if the path is not quite vertical), and a really crosswind flight, with no downwind move of the kite during all the climb while the full reel-out phase occurs.

9

The elevation angle for vertical trajectory (chapter 12, figure 12.17) looks to be higher than for figure-eight (Development and validation of a real time pumping kite model, figure 5-3, page 40 ). I do not know if some other curves could confirm it. If this is the case then the vertical trajectory allows the implementation of a shorter tether, hence an even less land use. Certainly however I would not say that this is the future of wind energy.

10

HorV
Choices on “vertical” are several.

11

image

The vertical trajectory in pumping mode on this topic concerns one of the types of verticals on the sketch above. The “Vertical Figure of 8” could not be used as a vertical trajectory such like described on this topic. Going down (during reel-in phase) in half eight doesn’t make sense.

12

The chapter 12 is available on

The vertical trajectory for Magnus Effect-Based AWES is described as I mentioned. See the Fig. 1.24 page 26, “Table 1.3 Parameters of the MW scale Magnus rotor” page 23, and page 24:

[…] the net output power is found to be 1.37 MW for X = 4.3, which corresponds to an energetic performance of 1.37 kW/m². This is consistent with the results of the medium scale system 1.48 kW/m² and 1.25 kW/m² found in [Milutinovic2015].

Now let us try to compare the efficiency (kW/m²) with also a Magnus Effect-Based AWES, but flying by “crosswind trajectories” (from the abstract of Modeling and control of a Magnus effect-based airborne
wind energy system in crosswind maneuvers https://hal.science/hal-01514058/document), the Fig. 6 page 7 representing a figure-eight. See also 4.2 Simulation parameters, then in page 8:

This results in a mean power of the full cycle of 1.47MW.

It can be assumed that the two Magnus-effect AWES have been optimized. The second one covers half the area for a comparable or even identical power.

My temporary comment: the vertical trajectory is also a crosswind trajectory, but it operates over only one side around the quasi center of the flight window compared to a horizontal crosswind trajectory. The other side would be underground… On the other hand, the vertical trajectory can start at a lower altitude, closer to the maximum power area of the flight window, but ends at a high elevation angle where the harvested power is lesser.

In the end, the horizontal crosswind trajectory has the advantage of being able to sweep the two sides around the quasi center of the flight window, which could explain the better performance in simulation, but at the cost, at least for the Magnus cylinder, of greater maneuvering complexity and a limit to scalability due to turn requirement.

1 Like
13

After the constructive criticism of the major disadvantages of a vertical trajectory with a power kite, I return to the Magnus effect balloon for which such a trajectory is planned, by presenting a method that I had outlined (see the three comments from the link): transmission not by two axes at the two ends, but by belts placed along the balloon, in order to limit the stresses on the structure to allow greater scaling.

I put again the video, after having reviewed some results. I measured (with a rpm-check) rpm 3200 with the 8 cm diameter wheel, by using a drill given to 500 W and rpm 3000, so 13.4 m/s tangential (wheel) velocity without the balloon, then rpm 2800-2900 with the balloon (about a max of rpm 240 for the balloon of 3 meters in circumference), so about 12 m/s tangential (wheel and balloon) velocity.

The decrease in speed with the balloon is therefore not enormous and corresponds to the margin of inaccuracy and losses due to oscillations (balloon not precisely centred), the belt more or less well tensioned, the shape of the balloon… This gave me (counting my own errors) 141 W instead of the theoretical 41 W according to the formula below which seems reliable to me. This is not so bad and it can be much improved with clearer material.

To evaluate the power consumption I use the formula “Power = Cf ρ U³ tan / 2 Area” indicated in the last page of the document below, where the tangential velocity is cubed, and Cf = 0.007:

The video (not new but deleted then put again):

A sketch for a larger balloon with several motors-belts and a long ground station:

Magnus balloon with external belts-motors connected to respective tethers
Magnus balloon with external belts-motors connected to respective tethers1286×1761 206 KB

The same with a small ground station:

Magnus balloon with external belts-motors

Drawbacks: without guides, the belts can go, and the balloon can escape. In this case a huge mass of air would travel around destroying everything in its path, unless one end could open and let the air out; slowness and time lag between stop (reel-in yoyo phase) and start (reel-out power yoyo phase); failure on one of the motors…

2 Likes
14

Me:

Some airborne wind energy systems are Magnus effect-based cylindrical balloons. Generally the balloon is held by the two axes settled in the respective two ends, and that the two motors rotate with the balloon, which leads to bending wind forces in the middle of the balloon, preventing scaling more. Have you heard of another transmission, using motorized belts surrounding the balloon and running along its entire span? Could this solve the problem?

ChatGPT:

I haven’t specifically heard of an airborne wind energy system that uses motorized belts surrounding the balloon and running along its entire span, but it’s possible that such a design could help address the issue of bending forces in the middle of the balloon.

By using motorized belts to rotate the balloon, rather than motors located at the ends of the balloon, the bending forces may be more evenly distributed along the entire length of the balloon, which could potentially reduce the risk of structural instability and improve scalability. Additionally, the use of belts could allow for more precise control over the rotation of the balloon, which could further improve the efficiency of the system.

However, it’s important to note that any new design or modification to an existing airborne wind energy system would need to be thoroughly tested and evaluated for safety, efficiency, and overall performance before it could be widely adopted.

Although I don’t think ChatGPT’s answers should be taken at face value at this stage, its rapid progress seems to be gradually becoming an asset towards the study of AWE projects, knowing the complexity of the evaluation often far beyond what one person can, just as calculating machines are useful aids.

2 Likes
15

The chapter 13 of the second AWE book is on https://www.researchgate.net/publication/324134888_Optimization-Inspired_Control_Strategy_for_a_Magnus_Effect-Based_Airborne_Wind_Energy_System/comments :

Optimization-Inspired Control Strategy for a Magnus Effect-Based Airborne Wind Energy System

Authors: * Milan MilutinovićMilan Milutinović

This chapter theorizes the vertical trajectory. Pages 313 and 314:

  1. The trajectory loop is almost vertical, as opposed to slant loops produced by the basic control strategy. Given the horizontal direction of the wind, this suggests that the ABM should fly in the crosswind direction, which was not immediately clear for this system. This was corroborated by conducting the optimization with slanted (non-horizontal) wind direction [14], which also produced a crosswind motion direction.
  2. The trajectory position in the xz-plane is quite far from the winch, more specifically as far as possible for the given tether length limit. This suggests the optimal operation is more easily achieved far from the winch and that this location influences power production (in fact, an earlier formulation clearly pointed out that vertical trajectory is practically unsustainable near the winch [14]).
  3. The results of the optimization, providing average power of 89.18 kW, are significantly better than the basic control strategy results, which produced average power of 40.15 kW. This means that an improvement of 122% has been achieved through optimal control. Note that the basic control strategy causes radial lift, in contrast with the vertical lift associated with the crosswind motion of the optimally controlled system.

The chapter 12 (Control of a Magnus Effect-Based Airborne
Wind Energy System) also investigates a vertical trajectory for Magnus balloon:
https://hal.science/hal-01759173/document
Authors: Ahmad Hably, Jonathan Dumon, Garrett Smith and Pascal Bellemain.

The figure 1.24 represents a 80 m span balloon and tether length from 200 m to 300 m, so a relatively low tether length, and a rectangular sweeping allowing to maximize the power / space consumption.

These two chapters are the foundations of this topic.

16

From the paper quoted above: “Experiments on a Flettner rotor at critical and supercritical Reynolds numbers”.

3.4. Power coefficient
The power necessary to spin the cylinder […]
Power = Cf ρ U³tan 2 . Area
A close agreement with the experimental results is found by setting
Cf = 0:007, that can be considered a reasonable value for the friction
coefficient.

Although this formula applies to well optimized rigid Magnus cylinders, the power consumption looks too high for Magnus crosswind kites in faster and theoretically more efficient horizontal flight. It is because the spin ratio must be related to the apparent wind speed which is much higher, even considering a modest glide number of 2.8.

Approximate calculations for some examples:
For a crosswind Magnus kite, the power consumption would be too high. Examples with a 1 m² cylinder (x 3.14) at 10 m/s wind speed, L/D ratio = 2.8 (favorable value deduced from Fig. 4 and Fig. 7), so kite speed = 28 m/s for examples 1 and 2 below, based on a rigid cylinder like that of “Experiments…”.

Example 1: spin ratio of 4, lift coefficient of 7 (Fig. 4) : power consumption = 0.007 x 1.2 x 112³ x 3.14/2 = 18528 W; power in pumping mode = only ½ x 1 x 2/27 x 1000 x 7 x 7.84 = 2032 W.

Example 2: if the spin ratio is only 2, the lift coefficient is 4 (Fig. 4), for a same L.D ratio of 2.8: power consumption = 0.007 x 1.2 x 56³ x 3.14/2 = 2316 W; power in pumping mode = only ½ x 1 x 2/27 x 1000 x 4 x 7.84 = 1161 W.

Example 3: in a (slower because smaller window flight) vertical flight, for a spin ratio of 1.21, lift coefficient of 2.3, same L.D ratio, power consumption = 0.007 x 1.2 x 10.21³ x 3.14/2 = 14 W; power in pumping mode = ½ x 1 x 2/27 x 1000 x 2.3 x 7.84/2 because we would loss about half of power in vertical crosswind flight: 334 W.

17

Today, by wind speed of 5 m/s, I experimented my 1 m² two line power kite, 0.2 kg without lines, 0.3 kg with 20 m lines, in vertical trajectory from bottom to top, and face to the wind in the middle of the wind window. Then I compared with horizontal trajectories one by one then chained into figure-eights, then loop.

The traction developed during vertical trajectories was significantly lower than that developed during the other figures, half for the best. This impression of little power during vertical trajectories was confirmed by my steelyard: 10 to 30 N, against 40 to 70 N for the other figures.

The gravity can be an explain. I noticed that every time the kite deviated from its vertical trajectory, it immediately gained additional power.

Another explanation, which I had to mention here and there, is that the horizontal trajectory is twice as long as the vertical trajectory, articulating on either side of the power zone, unlike the vertical trajectory ( which cannot go underground).

A version of the chapter 12 is available on:

See the figure 1.24. See also the 1.7 Conclusions and Perspectives page 25, mentioning a theoretical value of 1.48 kW/m². The chapter 13 stated that the vertical trajectory is more powerful than the conventional trajectory (for Magnus effect-based balloon).

But theoretical value for crosswind flight with figure-eight (not purely vertical trajectory) would be still higher, as stated on:

Table 2, balloon 40 x 12.5 = 500 m²; 5. CONCLUSIONS :

This results in a mean power of the full cycle of 1.47 MW.

So 2.94 kW/m².

1 Like
18

Hello Pierre: This is not surprising since flying crosswind increases the “swept area”.
The question would be whether the simpler version that does not fly crosswind might be lower cost and/or more reliable, to yield a better overall result.

One example would be farm windmills for pumping water. Newbies would think such a high-solidity rotor would be more efficient with all those blades, but the farm water-pumpers are about half as efficient as regular wind turbines and attempts to electrify them have fallen flat, since they use more material to give less power.

But for keeping a herd of cattle watered in a reliable way, especially if nobody is there to keep monitoring it in a daily basis, the efficiency is not as important as low-wind operation, consistent operation, and reliability, assuming yearly maintenance is performed.

So, depending on the use, such factors as dependability and reliability, and the ability to perform in low-speed winds can outweigh efficiency per se.

19

Flying crosswind can mean flying vertically or horizontally or both by figure-eight or loop. All these sorts of flying increase the “swept area” compared to a static kite (if we consider a static kite sweeps a wind area), but flying only vertically limits the usable flight window and divides it by two compared to flying only horizontally close to the ground.

20

Yes but in the case of kite-reeling and similar schemes, the vertical reel-out speed is usually low, compared to the crosswind (normally sideways) flight, so the sideways flight usually sweeps MORE area, which is why the redundant “million flies” of kite-reeling all tend to choose crosswind flight.