I agree. My “fact” answer to @dougselsam was only a circumstantial answer.
@WindFisher implements 2 motors per cable wrapping the cylinder. These motors are ground-based. They supply two respective winches via gears. By this the 2 motors ensure the rotation of the cylinder in the two directions, variations of the used length of the cable to achieve power and recovery phases for the reeling system, then also works as generators during power phase.
I think this would be applicable for the balloon described on this topic, using vertical trajectories. However this device is protected by the patent FR3123317A1.
Apart from that, it would be possible to reduce the problem (for other problems it is another story) of inertia mass compared with the “aero lift” by reducing the diameter, while retaining the maximum possible length, as in the balloon below:
The cables (as for the belts) allow some rigidity of the balloon. That said the Magnus balloon would not be so scalable.
The last writing of the preprint is lightly modified:
It turns out that pumping mode could be viable with the system described if the dimensions of a unit are limited (100-250 m long) due to the too high mass of air inertia as the balloon scales up. Ladders of stacked Magnus balloons are perhaps possible. That said the use as a stationary lifter (for PV or/and AWES) could allow to achieve higher dimensions.
Practically it could not compete with HAWT by far, in spite higher altitude winds would be harnessed.
Concerning the transmission for the vertical (a little crosswind) pumping mode, I prefer keep my initial plan with simple tethers for reel-out/in operations, and motorized belts with the motors aloft: these add weight in flight, but also stability by lowering the center of gravity, whereas simple tethers save weight.
This transmission system is well adapted for vertical trajectories or for a stationary flight as a lifter (balloon carrying PV or/and AWES), but not for horizontal trajectories due to the motors and the connection between the balloon and the ground station.
Lightly modified conclusion:
Conclusion
It turns out that pumping mode could perhaps be viable (but not compared to HAWT) with the system described if the dimensions of a unit are limited (100-250 m long) due to the too high mass of air inertia as the balloon scales up. Ladders of stacked Magnus balloons are perhaps possible. That said the use as a stationary lifter (for PV or/and AWES) could allow to achieve higher dimensions.
(PDF) Towards a gigantic Magnus balloon with motorized belts. Available from: https://www.researchgate.net/publication/371856926_Towards_a_gigantic_Magnus_balloon_with_motorized_belts [accessed Aug 10 2023].
I would like to reiterate I don’t agree to the explanation you have for dismissing this idea. not saying more than that positive or negative, but yeah. We could discuss it more if you feel like it
As the size of the balloon increases, all the dimensions increase at the same time in order to maintain the same aspect ratio. The power is therefore linked to the surface area (which increases with the square) of the cylinder, while the inertial mass is linked to the volume (which increases with the cube) of the cylinder. And thermal currents are not predictable. This limits the dimensions due to the resulting kinetic energy when descending or ascending with such a current. The vertical pumping mode is particularly affected.
In addition, a number of unknown factors can pose major problems, such as the force exerted on a huge balloon (even if it is “only” 250 m long), and the possible inequality of this force. The adjustment between the multi-anchored long station and the balloon itself can be difficult.
Since, overall, I have not found a density per km² greater than that of a conventional wind farm, I conclude that such a system is unlikely to be viable, given the reliability and safety which are inevitably inferior to those of HAWT, the unknown factors, and the space required, which cannot be reduced to ground stations alone. These are the problems inherent in AWES, and those specific to this system.
So that leads to a magnitude more resulting in increased volume (inertial mass) vs increased area (power).The volume will increase ten times more than the useful surface area (length x diameter) for wind force and power.
Your “10x longer distance” matches my “The inertial mass increases with the volume, so a magnitude more than the “aero lift ” which increases with the area.” As a result, this device cannot scale beyond some limits as explained above and in some previous comments I wrote including this one.
Now a possibility could be making a thinner balloon, increasing its length while reducing the diameter, or stacking them. Other problems can occur such like the control, the lack of volume for efficient heating, and also some advantages such like more centrifugal force projecting colder air towards the inner walls, but there are only assumptions.
And also a good density per km² could be achieved even if scaling is limited, although I think scaling (in the dimensions or by the swept area) is a key, because that leads to less unities, thus less tether problems and mess risk.
Please can you explain why?
So I tried to explain this but discarded my draft as an analysis depends on knowing about magnus effect scaling, something I don’t have, at least not readily available. I could obtain that info but it would take me many hours of work and I am not ready to invest that kind of effort here.
To be clear I think the design does not really appeal to me. But the reasons it shouldn’t work are mostly mechanical and not my speciality, so I would not be the right person to point out such problems. It is an interesting idea though, and I like the fact that you are thinking big here.
So my analysis goes something like this, this time leaving out magnus related (important) stuff:
In my experience with AWE, most things scale well except mass. I start by assuming the whole think working as a given size, then scale everything by a factor x and see what comes out.
So, I would think:
- The reel out speed is dependent on wind speed and stays constant
- The tether length scales by x
- The tether length difference min to max in the cycle scales by x
- The time per cycle scales by x
- The time it takes to accellerate/decellerate scales by x, up an down that is (*). This is ok due to the previous point
- The time it takes to spin/unspin the magnus cylinder must also scale with x for scaling to be neutral. This though is complicated to evaluate, I don’t know this one
Given the points above it seems to me a fair chance the design i scaling neutral. The mass of the air inside the cylinder scales, but could not affect bouyancy as you have air on the inside and air on the outside. On the contrary, bouyancy is infact better with scale if you want heated air inside the cylinder, due to less heat dissipation of large bodies and more volume per «wing area».
(*) Acceleration is a = \frac{F}{m}. The lift force F scales by x^2 and the mass of the air x^3
Anyways, this analysis so far points me to scaling neutrality. The only thing I didnt really consider is the known issue of skin thickness scaling that must occur at one point, after which you have cubic mass scaling. But maybe that scale is humongous?
Now relating to the time needed to spin/unspin the cylinder. The moment of inertia of a cylinder scales x^3. But in this case we should not neglect that the air inside the cylinder does not need to stop rotating even if the magnus cylinder skin stops rotating. Also, what is the rotational speed \omega of the cylinder? I believe maybe the magnus effect depends on skin speed vs wind speed. In that case the rotational speed \omega would probably scale by a factor \frac{1}{x}. But what is the scaling of your ability to alter rotational speed? So perhaps the time to spin/unspin could be anywhere from positive-neutral-negative from a scaling point of view. One could calculate this quite simply though given some days of work, simulations and the necessary knowhow.
All in all, I dont understand your arguments about the thing falling down at scale due to thermals. Being bigger and slower, probably it would become more immune to thermals as you have more time to even them out, and also thermal and other turbulences would be limited in size. If they are much smaller than the cylinder maybe they dont matter much?
I would also like to point out that if anyone is every to succeed in AWE there are many of these kinds of hurdles to be jumped. At this point we dont even know how many hurdles there are. But for sure «giving up» is the one quality almost guaranteeing failure. On the other hand, pursuing the wrong ideas is also likely to fail. And here we are ![]()
Hi @tallakt , thank you for your work.
I can agree for the almost, letting some unknowns as we can agree.
My purpose was to start from related Omnidea experiments, with about 5-6 m/s wind speed and a spin ratio (tangential speed of the spin cylinder/wind speed) of 1.21, then try to extrapolate with a wind speed of 10 m/s for the same spin ratio, then with a spin ratio of 2. Beyond the power consumption was too high.
For scaling, I preferred the implementation of the motorized belts along the balloon.
This looks correct to me. Perhaps I was wrong to worry about the phases slowing down when the cycle itself is longer, when the balloon scales up.
As (air) mass increases, so does inertia. In a sense you’re right: a large balloon will resist thermals better thanks to its inertia… until the moment when a thermal that’s too strong ends up dragging it along without being able to stop it, because of its inertia.
As I can’t go any further with this idea (scaling by using motorized belts), because I don’t have what is required to make a serious prototype, I’m putting it aside either to take it up again later, or for someone else to do it if they feel like it, or to abandon it.
In addition to all this, I would add that I see at least four ways of scaling for an unit or a AWES farm: Scaling by size (as for this Magnus balloon), Scaling in numbers rather than size, Kite Networks, AWES farm in bumper car mode (allowing more density, perhaps possible with Magnus balloons in the case of no damage due to possible collisions).
This video gives some good points on the difficulties and perhaps impossibilities involved: Should Airships Make a Comeback? - Veritasium
The two statements overlap. Scaling is therefore detrimental to control and safety because the air mass (and kinetic energy) increases by a magnitude more than lift.
Well the way I see it it needs linearly more time to change the spin. Which is not a problem as the distance usee for the flight pattern also increases linearly.
A difficulty of the blimp (in contrast to semi-rigid and rigid) is mentioned at 5:10. I reproduced the text below:
Like a balloon it is over-pressurized to maintain its shape. Therefore, the skin of a blimp is in constant tension. As the blimp becomes larger, this tension increases. Moreover it becomes increasingly difficult for large blimps to maintain their shape. So you can’t scale up blimps forever.
The Magnus balloon, such as described on the preprint and discussed on this topic, can be seen as a blimp. The load is the wind force transmitted by the tethers instead of the mass of goods transported.
Spinning power consumption can be expected to increase proportionately more as the balloon scales up, due to increasing deformations of its shape.
I agree for the relation between the time to stop the spin and the flight pattern both increasing linearly.
That said the volume (leading to inertia mass, moment of inertia and kinetic energy) increases by the cube while the surface area (which determines aerodynamic lift) increases only by the square, which in practice limits the scalability of the balloon, because the lift becomes too low in order to counter the kinetic energy when a thermal current in the same direction occurs, or also if the wind stops blowing.
However this problem really occurs when the dimensions of the balloon are very large, probably far beyond the limit of scalability due to the flexible blimp type construction. Until really gigantic dimensions, the aerodynamic lift dominates the air mass.
This aspect I can’t comment usefully. I agree in general building larger and larger structures that maintain their shape is increasingly difficult.
The problem I am most worried about in this respect is the shear forces on the skin when applying moments to the stiff [inflated] end plates of the cylinder.
Shear forces on the discs (whose end plates) along the balloon by the (flat) belts, and on the skin by the discs themselves. All the discs (which have a dual function, aerodynamic and passage of belts) would be sewn on the fabric envelope.
About scalability, airship techniques solve the scalability problems of blimps by using rigid structures, as shown from 5:02. Perhaps a Tensairity ™ beam (with fans to keep the pressure) could improve scalability.
I noted that the energy consumption for an inflatable cylinder is much higher (because of the wind which hollows the balloon and slows it down in its rotation?) than that of rigid cylinders like those of Anemoi or others for ships. As a result for an AWE use, the spin ratio is more limited, just like the lift coefficient which increases when the spin ratio increases. And Tensairity ™ use increases the stiffness of the balloon, but not much the internal pressure: so we can guess that the energy consumption would remain high.
This gigantic Magnus balloon with externally motorized belts could perhaps consume less energy by being stiffer due to higher internal pressure by using shapewave® or drop-stitch style technologies for the beam used as a rotational cylinder. Thus a higher spin ratio could perhaps be achieved by consuming less energy.
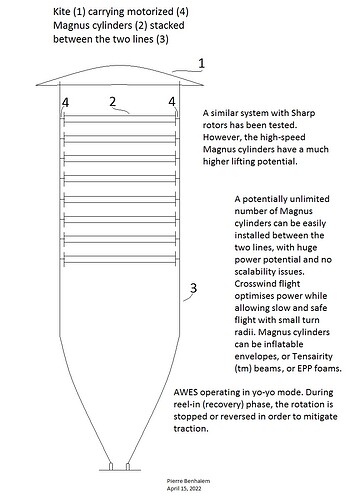
This could also be applied for much smaller stacked Magnus balloons between several tethers or stacked Magnus (instead of Sharp) balloons between only two tethers and possibly under a kite (sketch below: the kite is retained to aid takeoff, but it could perhaps be removed, vertical crosswind flight easier), mitigating inertia issue for a same overall area of balloons and therefore a lower overall volume.
Installing the Magnus Flettner balloons between paired tethers like mentioned above and like I did with Sharp rotors, is a natural mean to avoid any heavy frame for each balloon which is held in rotation by its two ends within its respective paired tethers.
Apart from this, the balloons could be heated by their respective motors of rotation if it is required.
If powered, spinning sausages are a better choice than airfoils for lift, why is there no airplane with spinning cylindrical wings, after all these 100 years?
The concept of the Flettner rotor was first devised by Finnish inventor and architect Sigurd Savonius and German engineer Anton Flettnerin the 1920s . The first Atlantic crossing – by a vessel using Flettner rotors only – took place in 1926.
And by the way, Goodyear built airplanes with inflatable wings 66 years ago: